
【題目】已知過點(diǎn)![]() 的直線l:
的直線l:![]() 與拋物線E:
與拋物線E:![]() (
(![]() )交于B,C兩點(diǎn),且A為線段
)交于B,C兩點(diǎn),且A為線段![]() 的中點(diǎn).
的中點(diǎn).
(1)求拋物線E的方程;
(2)已知直線![]() :
:![]() 與直線l平行,過直線
與直線l平行,過直線![]() 上任意一點(diǎn)P作拋物線E的兩條切線,切點(diǎn)分別為M,N,是否存在這樣的實(shí)數(shù)m,使得直線
上任意一點(diǎn)P作拋物線E的兩條切線,切點(diǎn)分別為M,N,是否存在這樣的實(shí)數(shù)m,使得直線![]() 恒過定點(diǎn)A?若存在,求出m的值;若不存在,說明理由.
恒過定點(diǎn)A?若存在,求出m的值;若不存在,說明理由.
【答案】(1)![]() ;(2)存在實(shí)數(shù)
;(2)存在實(shí)數(shù)![]() 使得命題成立
使得命題成立
【解析】
(1)直線方程與拋物線方程聯(lián)立,借助韋達(dá)定理![]() 即可求得
即可求得![]() ,得出拋物線方程;
,得出拋物線方程;
(2)設(shè)M,N點(diǎn)的坐標(biāo)分別為![]() ,
,![]() ,直線
,直線![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() ,由
,由 ,利用導(dǎo)數(shù)的幾何意義可得點(diǎn)M處的切線
,利用導(dǎo)數(shù)的幾何意義可得點(diǎn)M處的切線![]() 方程和點(diǎn)N處的切線
方程和點(diǎn)N處的切線![]() 方程,由
方程,由![]() 都滿足上述兩個(gè)方程,即有
都滿足上述兩個(gè)方程,即有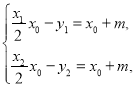 可得直線
可得直線![]() 的方程即為:
的方程即為:![]() ,點(diǎn)
,點(diǎn)![]() 代入即可得出存在實(shí)數(shù)
代入即可得出存在實(shí)數(shù)![]() 使得命題成立.
使得命題成立.
(1)由![]() ,
,![]() ,
,![]() ,
,
依題意![]() ,
,![]() .
.
故拋物線E的方程為:![]() .
.
(2)設(shè)M,N點(diǎn)的坐標(biāo)分別為![]() ,
,![]() ,直線
,直線![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() ,
,
由 ,可得點(diǎn)M處的切線
,可得點(diǎn)M處的切線![]() 的方程為:
的方程為:![]() ,
,
點(diǎn)N處的切線![]() 的方程為:
的方程為:![]()
∵![]() 都滿足上述兩個(gè)方程,∴
都滿足上述兩個(gè)方程,∴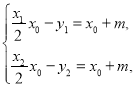
∴直線![]() 的方程為:
的方程為:![]() ,
,
∵直線![]() 恒過定點(diǎn)
恒過定點(diǎn)![]() ,∴
,∴![]() ,得
,得![]() ,
,
故存在實(shí)數(shù)![]() 使得命題成立.
使得命題成立.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
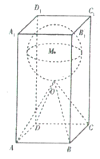
【題目】在日常生活中,石子是我們經(jīng)常見到的材料,比如在各種建筑工地或者建材市場上常常能看到堆積如山的石子,它的主要成分是碳酸鈣.某雕刻師計(jì)劃在底面邊長為2m、高為4m的正四棱柱形的石料![]() 中,雕出一個(gè)四棱錐
中,雕出一個(gè)四棱錐![]() 和球M的組合體,其中O為正四棱柱的中心,當(dāng)球的半徑r取最大值時(shí),該雕刻師需去除的石料約重___________kg.(最后結(jié)果保留整數(shù),其中
和球M的組合體,其中O為正四棱柱的中心,當(dāng)球的半徑r取最大值時(shí),該雕刻師需去除的石料約重___________kg.(最后結(jié)果保留整數(shù),其中![]() ,石料的密度
,石料的密度![]() ,質(zhì)量
,質(zhì)量![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓![]() 的右頂點(diǎn)為A,上頂點(diǎn)為B.已知橢圓的離心率為
的右頂點(diǎn)為A,上頂點(diǎn)為B.已知橢圓的離心率為![]() ,
,![]() .
.
(1)求橢圓的方程;
(2)設(shè)直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點(diǎn),
兩點(diǎn),![]() 與直線
與直線![]() 交于點(diǎn)M,且點(diǎn)P,M均在第四象限.若
交于點(diǎn)M,且點(diǎn)P,M均在第四象限.若![]() 的面積是
的面積是![]() 面積的2倍,求
面積的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知過點(diǎn)![]() 的直線l:
的直線l:![]() 與拋物線E:
與拋物線E:![]() (
(![]() )交于B,C兩點(diǎn),且A為線段
)交于B,C兩點(diǎn),且A為線段![]() 的中點(diǎn).
的中點(diǎn).
(1)求拋物線E的方程;
(2)已知直線![]() :
:![]() 與直線l平行,過直線
與直線l平行,過直線![]() 上任意一點(diǎn)P作拋物線E的兩條切線,切點(diǎn)分別為M,N,是否存在這樣的實(shí)數(shù)m,使得直線
上任意一點(diǎn)P作拋物線E的兩條切線,切點(diǎn)分別為M,N,是否存在這樣的實(shí)數(shù)m,使得直線![]() 恒過定點(diǎn)A?若存在,求出m的值;若不存在,說明理由.
恒過定點(diǎn)A?若存在,求出m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側(cè)面ABB1A1是邊長為2的菱形,且CA=CB1.
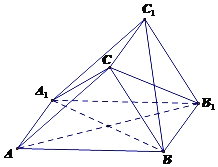
(1)證明:面CBA1⊥面CB1A;
(2)若∠BAA1=60°,A1C=BC=BA1,求點(diǎn)C到平面A1BC1的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
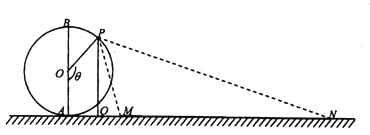
【題目】如圖,摩天輪的半徑![]() 為
為![]() ,它的最低點(diǎn)
,它的最低點(diǎn)![]() 距地面的高度忽略不計(jì).地上有一長度為
距地面的高度忽略不計(jì).地上有一長度為![]() 的景觀帶
的景觀帶![]() ,它與摩天輪在同一豎直平面內(nèi),且
,它與摩天輪在同一豎直平面內(nèi),且![]() .點(diǎn)
.點(diǎn)![]() 從最低點(diǎn)
從最低點(diǎn)![]() 處逆時(shí)針方向轉(zhuǎn)動到最高點(diǎn)
處逆時(shí)針方向轉(zhuǎn)動到最高點(diǎn)![]() 處,記
處,記![]() .
.
(1)當(dāng)![]() 時(shí),求點(diǎn)
時(shí),求點(diǎn)![]() 距地面的高度
距地面的高度![]() ;
;
(2)試確定![]() 的值,使得
的值,使得![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的最大值為
的最大值為![]() ,且曲線
,且曲線![]() 在x=0處的切線與直線
在x=0處的切線與直線![]() 平行(其中e為自然對數(shù)的底數(shù)).
平行(其中e為自然對數(shù)的底數(shù)).
(1)求實(shí)數(shù)a,b的值;
(2)如果![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com