
【題目】設區間![]() ,定義在
,定義在![]() 上的函數
上的函數![]() (
(![]() ),集合
),集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)設常數![]() .
.
① 討論![]() 的單調性;
的單調性;
② 若![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() (2)①見解析;②見證明
(2)①見解析;②見證明
【解析】
(1)把b![]() 代入函數解析式,求出導函數,由f′(x)
代入函數解析式,求出導函數,由f′(x)![]() 0,可知f(x)在[﹣3,3]上為增函數,求出函數的最小值,由最小值大于0求得a的取值范圍;
0,可知f(x)在[﹣3,3]上為增函數,求出函數的最小值,由最小值大于0求得a的取值范圍;
(2)①求出函數的導函數,解得導函數的零點,然后根據![]() 與3的關系分類求得函數的單調區間;
與3的關系分類求得函數的單調區間;
②當b<﹣1時,由①可知,當0<a![]() 時,求得函數的最小值小于0,得到矛盾,故此時實數a不存在;當a
時,求得函數的最小值小于0,得到矛盾,故此時實數a不存在;當a![]() 時,由①可得f(x)min={f(﹣3),f(
時,由①可得f(x)min={f(﹣3),f(![]() )},得到f(﹣3)<0,這與x∈D,f(x)≥0恒成立矛盾,故此時實數a不存在;若f(﹣3)>0,證明f(
)},得到f(﹣3)<0,這與x∈D,f(x)≥0恒成立矛盾,故此時實數a不存在;若f(﹣3)>0,證明f(![]() )<0,這與x∈D,f(x)≥0恒成立矛盾,故此時實數a不存在.
)<0,這與x∈D,f(x)≥0恒成立矛盾,故此時實數a不存在.
(1)當![]() 時,
時,![]() ,則
,則![]() .
.
由![]() 可知
可知![]() 恒成立,故函數
恒成立,故函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,解得
,解得![]() ,
,
所以集合![]()
(2)① 由![]() 得
得![]() ,
,
因為![]() ,則由
,則由![]() ,得
,得![]() .
.
在![]() 上列表如下:
上列表如下:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 單調遞增 | 極大值 | 單調遞減 | 極小值 | 單調遞增 |
(ⅰ)當![]() ,即
,即![]() 時,
時,
則![]() ,所以
,所以![]() 在
在![]() 上單調遞減;
上單調遞減;
(ⅱ)當![]() ,即
,即![]() 時,此時
時,此時![]() ,
,
![]() 在
在![]() 和
和![]() 上單調遞增;在
上單調遞增;在![]() 上單調遞減.
上單調遞減.
綜上,當![]() 時,
時,![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調遞增;
上單調遞增;
在![]() 上單調遞減
上單調遞減
②(方法一)當![]() 時,由①可知,
時,由①可知,
(ⅰ)當![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,
,
這與![]() 恒成立矛盾,故此時實數
恒成立矛盾,故此時實數![]() 不存在;
不存在;
(ⅱ)當![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調遞增;
上單調遞增;
在![]() 上單調遞減,
上單調遞減,
所以![]() .
.
若![]() ,這與
,這與![]() 恒成立矛盾,
恒成立矛盾,
故此時實數![]() 不存在;
不存在;
若![]() ,此時
,此時![]() ,
,
又![]() ,則
,則![]() ,
,
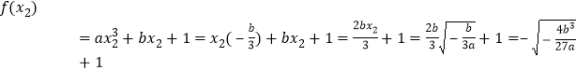 .
.
下面證明![]() ,也即證:
,也即證:![]() .
.
因為![]() ,且
,且![]() ,則
,則![]() ,
,
下證:![]() .
.
令![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,即
,即![]() .
.
這與![]() 恒成立矛盾,故此時實數
恒成立矛盾,故此時實數![]() 不存在.
不存在.
綜上所述,![]() .
.
(方法二)(ⅰ)當![]() 時,
時,![]() 成立;
成立;
(ⅱ)當![]() 時,由題意可知
時,由題意可知![]() 恒成立,則
恒成立,則![]() ,
,
設![]() ,則
,則![]() ,
,
令![]() ,解得
,解得![]() .
.
因為![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() ,所以
,所以![]() ;
;
(ⅲ)當![]() 時,由題意可知
時,由題意可知![]() 恒成立,則
恒成立,則![]() .
.
設![]() ,則
,則![]() ,
,
因為![]() ,所以
,所以![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,
,
所以![]() .
.
若![]() ,則存在實數
,則存在實數![]() 滿足
滿足![]() ,
,
則![]() 成立,即
成立,即![]() ,
,
也即![]() 成立,
成立,
則![]() ,這與
,這與![]() 矛盾,所以
矛盾,所以![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源: 題型:
【題目】《九章算術》卷第五《商功》中有記載:“芻甍者,下有袤有廣,而上有袤無廣.芻,草也.甍,屋蓋也.”翻譯為“底面有長有寬為矩形,頂部只有長沒有寬為一條棱.芻甍字面意思為茅草屋頂.”現有一個芻甍,如圖,四邊形![]() 為正方形,四邊形
為正方形,四邊形![]() 、
、![]() 為兩個全等的等腰梯形,
為兩個全等的等腰梯形,![]() ,
,![]() ,若這個芻甍的體積為
,若這個芻甍的體積為![]() ,則
,則![]() 的長為( )
的長為( )
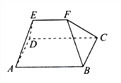
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點.研究表明:“活水圍網”養魚時,某種魚在一定的條件下,每尾魚的平均生長速度![]() (單位:千克/年)是養殖密度
(單位:千克/年)是養殖密度![]() (單位:尾/立方米)的函數.當
(單位:尾/立方米)的函數.當![]() 時,
時,![]() 的值為2千克/年;當
的值為2千克/年;當![]() 時,
時,![]() 是
是![]() 的一次函數;當
的一次函數;當![]() 時,因缺氧等原因,
時,因缺氧等原因,![]() 的值為0千克/年.
的值為0千克/年.
(1)當![]() 時,求
時,求![]() 關于
關于![]() 的函數表達式.
的函數表達式.
(2)當養殖密度![]() 為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
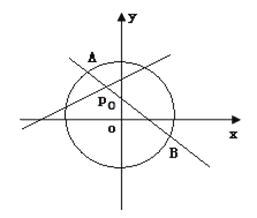
【題目】已知圓O:x2+y2=8內有一點P0(﹣1,2),AB為過點P0且傾斜角為α的弦.
(1)當α=135°時,求弦AB的長;
(2)當弦AB被P0平分時,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖像關于直線
的圖像關于直線![]() 對稱,且
對稱,且![]() .
.
(1)求![]() 的表達式;
的表達式;
(2)若將![]() 圖像上各點的橫坐標變為原來的
圖像上各點的橫坐標變為原來的![]() ,再將所得圖像向右平移
,再將所得圖像向右平移![]() 個單位,得到
個單位,得到![]() 的圖像,且關于
的圖像,且關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有且只有一個實數解,求實數
上有且只有一個實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第二屆中國國際進口博覽會于2019年11月5日至10日在上海國家會展中心舉行,來自151個國家和地區的3617家企業參展,規模和品質均超過首屆.更多新產品、新技術、新服務“全球首發,中國首展”,專(業)精(品)尖(端)特(色)產品精華薈萃.某跨國公司帶來了高端空調模型參展,通過展會調研,中國甲企業計劃在2020年與該跨國公司合資生產此款空調.生產此款空調預計全年需投入固定成本260萬元,每生產x千臺空調,需另投入資金![]() 萬元,且
萬元,且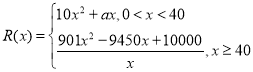 .經測算生產10千臺空調需另投入的資金為4000萬元.由調研知,每臺空調售價為0.9萬元時,當年內生產的空調當年能全部銷售完.
.經測算生產10千臺空調需另投入的資金為4000萬元.由調研知,每臺空調售價為0.9萬元時,當年內生產的空調當年能全部銷售完.
(1)求2020年的企業年利潤![]() (萬元)關于年產量x(千臺)的函數關系式;
(萬元)關于年產量x(千臺)的函數關系式;
(2)2020年產量為多少(千臺)時,企業所獲年利潤最大?最大年利潤是多少?注:利潤=銷售額–成本
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為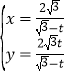 (
(![]() 為參數,且
為參數,且![]() ),以坐標原點為極點,
),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 的參數方程化為普通方程,并將曲線
的參數方程化為普通方程,并將曲線![]() 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(2)求曲線![]() 與曲線
與曲線![]() 交點的極坐標
交點的極坐標![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com