
【題目】已知函數![]() .
.
(1)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(2)若不等式![]()
![]() 對于任意
對于任意![]() 成立,求正實數
成立,求正實數![]() 的取值范圍.
的取值范圍.
【答案】(1)答案見解析;(2) ![]() .
.
【解析】試題分析: ![]() 求出函數的定義域和導數,然后討論當
求出函數的定義域和導數,然后討論當![]() 時,當
時,當![]() 時確定
時確定![]() 的單調性
的單調性![]() 問題等價于對任意
問題等價于對任意![]() ,有
,有![]() 成立,設
成立,設![]() ,
, ![]() ,根據函數的單調性求出
,根據函數的單調性求出![]() 的最大值,解關于
的最大值,解關于![]() 的不等式,解出即可
的不等式,解出即可
解析:(1)函數![]() 的定義域為
的定義域為![]() .
.
![]()
![]()
![]() .
.
若![]() ,則
,則
當![]() 或
或![]() 時,
時, ![]() ,
, ![]() 單調遞增;
單調遞增;
當![]() 時,
時, ![]() ,
, ![]() 單調遞減.
單調遞減.
若![]() ,則
,則
當![]() 時,
時, ![]() ,
, ![]() 單調遞減;
單調遞減;
當![]() 時,
時, ![]() ,
, ![]() 單調遞增.
單調遞增.
綜上所述,當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;當
上單調遞減;當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 和
和![]() 上單調遞增.
上單調遞增.
(2)原題等價于對任意![]() ,有
,有![]() 成立.
成立.
設![]() ,
, ![]() ,所以
,所以![]() .
.
![]()
![]() .
.
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
所以函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
![]() 為
為![]() 與
與![]() 中的較大者.
中的較大者.
設![]()
![]() ,
,
則![]()
![]() ,
,
所以![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]() ,所以
,所以![]() ,
,
從而![]() .
.
所以![]() 即
即![]() .
.
設![]() ,則
,則![]() .
.
所以![]() 在
在![]() 上單調遞增.
上單調遞增.
又![]() ,所以
,所以![]() 的解為
的解為![]() .
.
因為![]() ,所以正實數
,所以正實數![]() 的取值范圍為
的取值范圍為![]() .
.


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源: 題型:
【題目】采用系統抽樣方法從![]() 人中抽取
人中抽取![]() 人做問卷調查,為此將他們隨機編號為
人做問卷調查,為此將他們隨機編號為![]() ,
,![]() ,
,![]() ,
,![]() ,分組后某組抽到的號碼為41.抽到的
,分組后某組抽到的號碼為41.抽到的![]() 人中,編號落入區間
人中,編號落入區間![]() 的人數為( )
的人數為( )
A. 10 B. ![]() C. 12 D. 13
C. 12 D. 13
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】針對“中學生追星問題”,某校團委對“學生性別和中學生追星是否有關”作了一次調查,其中女生人數是男生人數的![]() ,男生追星的人數占男生人數的
,男生追星的人數占男生人數的![]() ,女生追星的人數占女生人數的
,女生追星的人數占女生人數的![]() .若有
.若有![]() 的把握認為是否追星和性別有關,則男生至少有( )
的把握認為是否追星和性別有關,則男生至少有( )
參考數據及公式如下:
|
|
|
|
|
|
|
|
![]()
A. 12B. 11C. 10D. 18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“黃梅時節家家雨”“梅雨如煙暝村樹”“梅雨暫收斜照明”……江南梅雨的點點滴滴都流潤著濃烈的詩情.每年六、七月份,我國長江中下游地區進入持續25天左右的梅雨季節,如圖是江南![]() 鎮2009~2018年梅雨季節的降雨量(單位:
鎮2009~2018年梅雨季節的降雨量(單位:![]() )的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:
)的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:

![]() “梅實初黃暮雨深”.請用樣本平均數估計
“梅實初黃暮雨深”.請用樣本平均數估計![]() 鎮明年梅雨季節的降雨量;
鎮明年梅雨季節的降雨量;
![]() “江南梅雨無限愁”.
“江南梅雨無限愁”.![]() 鎮的楊梅種植戶老李也在犯愁,他過去種植的甲品種楊梅,他過去種植的甲品種楊梅,畝產量受降雨量的影響較大(把握超過八成).而乙品種楊梅2009~2018年的畝產量(
鎮的楊梅種植戶老李也在犯愁,他過去種植的甲品種楊梅,他過去種植的甲品種楊梅,畝產量受降雨量的影響較大(把握超過八成).而乙品種楊梅2009~2018年的畝產量(![]() /畝)與降雨量的發生頻數(年)如
/畝)與降雨量的發生頻數(年)如![]() 列聯表所示(部分數據缺失).請你幫助老李排解憂愁,他來年應該種植哪個品種的楊梅受降雨量影響更小?
列聯表所示(部分數據缺失).請你幫助老李排解憂愁,他來年應該種植哪個品種的楊梅受降雨量影響更小?
(完善列聯表,并說明理由).
畝產量\降雨量 |
|
| 合計 |
<600 | 2 | ||
| 1 | ||
合計 | 10 |
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.703 |
(參考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 是各項均為正數的數列
是各項均為正數的數列![]() 的前
的前![]() 項和,且
項和,且![]() .
.
(1)求![]() 的值;
的值;
(2)設![]() ,且數列
,且數列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() 對任意正整數
對任意正整數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)設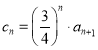 ,問:是否存在正整數
,問:是否存在正整數![]() ,使得
,使得![]() 對一切正整數
對一切正整數![]() 恒成立?若存在,請求出實數
恒成立?若存在,請求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com