
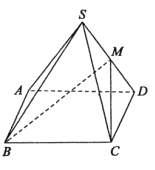
【題目】已知四棱錐![]() ,四邊形
,四邊形![]() 是正方形,
是正方形, ![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 的中點,求二面角
的中點,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2) ![]()
【解析】試題分析:(1)由![]() 可得
可得![]() ,即
,即![]() ,由
,由![]() 為正方形,可得
為正方形,可得![]() ,從而得
,從而得![]() 平面
平面![]() ,由面面垂直的判定定理可得平面
,由面面垂直的判定定理可得平面![]() 平面
平面![]() ;(2)設
;(2)設![]() 的中點為
的中點為![]() ,∵
,∵![]() ,∴
,∴![]() ,面面垂直的性質可得
,面面垂直的性質可得![]() 平面
平面![]() ,在平面
,在平面![]() 內,過
內,過![]() 作直線
作直線![]() ,則
,則![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,
為坐標原點, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸,建立空間直角坐標系,分別根據向量垂直數量積為零列方程組求出平面
軸,建立空間直角坐標系,分別根據向量垂直數量積為零列方程組求出平面![]() 與平面
與平面![]() 的一個法向量,根據空間向量夾角余弦公式,可得結果.
的一個法向量,根據空間向量夾角余弦公式,可得結果.
試題解析:(1)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() 為正方形,∴
為正方形,∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)
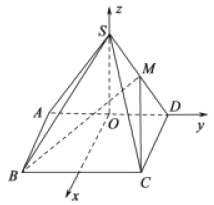
設![]() 的中點為
的中點為![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
由(1)可知平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
在平面![]() 內,過
內,過![]() 作直線
作直線![]() ,則
,則![]() 兩兩垂直.
兩兩垂直.
以![]() 為坐標原點,
為坐標原點, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
則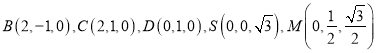 ,
,
∴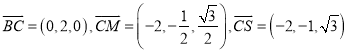 ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,
, 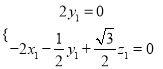 ,即
,即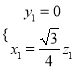 ,取
,取![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,
, 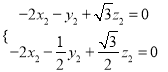 ,即
,即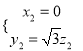 ,取
,取![]() ,
,
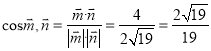 ,由圖可知,二面角
,由圖可知,二面角![]() 的余弦值為
的余弦值為![]() .
.
【方法點晴】本題主要考查面面垂直的判定定理以及利用空間向量求二面角,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() :
: ![]() .
.
(1)已知直線![]() 與雙曲線
與雙曲線![]() 交于不同的兩點
交于不同的兩點![]() ,且
,且![]() ,求實數
,求實數![]() 的值;
的值;
(2)過點![]() 作直線
作直線![]() 與雙曲線
與雙曲線![]() 交于不同的兩點
交于不同的兩點![]() ,若弦
,若弦![]() 恰被點
恰被點![]() 平分,求直線
平分,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】遂寧市觀音湖港口船舶停靠的方案是先到先停.
(1)若甲乙兩艘船同時到達港口,雙方約定各派一名代表從1,2,3,4,5中各隨機選一個數(甲、乙選取的數互不影響),若兩數之和為偶數,則甲先停靠;若兩數之和為奇數,則乙先停靠,這種規則是否公平?請說明理由.
(2)根據以往經驗,甲船將于早上7:00~8:00到達,乙船將于早上7:30~8:30到達,請求出甲船先停靠的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分圖象如圖所示. 
(1)求f(x)的解析式,并求函數f(x)在[﹣ ![]() ,
, ![]() ]上的值域;
]上的值域;
(2)在△ABC中,AB=3,AC=2,f(A)=1,求sin2B.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩俱樂部舉行乒乓球團體對抗賽.雙方約定:
①比賽采取五場三勝制(先贏三場的隊伍獲得勝利.比賽結束)
②雙方各派出三名隊員.前三場每位隊員各比賽﹣場
已知甲俱樂部派出隊員A1、A2 . A3 , 其中A3只參加第三場比賽.另外兩名隊員A1、A2比賽場次未定:乙俱樂部派出隊員B1、B2 . B3 , 其中B1參加第一場與第五場比賽.B2參加第二場與第四場比賽.B3只參加第三場比賽
根據以往的比賽情況.甲俱樂部三名隊員對陣乙俱樂部三名隊員獲勝的概率如表:
A1 | A2 | A3 | |
B1 |
|
|
|
B2 |
|
|
|
B3 |
|
|
|
(1)若甲俱樂部計劃以3:0取勝.則應如何安排A1、A2兩名隊員的出場順序.使得取勝的概率最大?
(2)若A1參加第一場與第四場比賽,A2參加第二場與第五場比賽,各隊員每場比賽的結果互不影響,設本次團體對抗賽比賽的場數為隨機變量X,求X的分布列及數學期望E(X)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,空間四邊形ABCD的對棱AD、BC成600的角,且AD=BC=a,平行于AD與BC的截面分別交AB、AC、CD、BD于E、F、G、H.
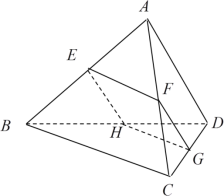
(1)求證:四邊形EFGH為平行四邊形;
(2)E在AB的何處時截面EFGH的面積最大?最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商品在近30天內每件的銷售價格P元和時間t(t∈N)的關系如圖所示.
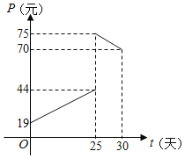
(1)請確定銷售價格P(元)和時間t(天)的函數解析式;
(2)該商品的日銷售量Q(件)與時間t(天)的關系是:Q=﹣t+40(0≤t≤30,t∈N),求該商品的日銷售金額y(元)與時間t(天)的函數解析式;
(3)求該商品的日銷售金額y(元)的最大值,并指出日銷售金額最大的一天是30天中的哪一天?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com