函數f(x)=lg(x2-ax-1)在區間(1,+∞)上為單調增函數,則a的取值范圍是 .
【答案】
分析:利用復合函數的單調性遵循的規律:同增異減判斷出t的單調性;對數的真數大于0得到不等式恒成立;利用二次函數的單調性與對稱軸有關及不等式恒成立轉化為最值問題.
解答:解:令t=x
2-ax-1則y=lgt
∵y=lgt在(0,+∞)遞增
又∵函數f(x)=lg(x
2-ax-1)在區間(1,+∞)上為單調增函數,
∴t=x
2-ax-1在區間(1,+∞)上為單調增函數,且 x
2-ax-1>0在(1,+∞)恒成立
所以
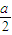
≤1且1-a-1≥0
解得a≤0
故答案為a≤0
點評:本題考查復合函數的單調性遵循的規律:同增異減、考查二次函數的單調性與對稱軸有關、考查不等式恒成立轉化為函數最值的范圍.

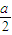 ≤1且1-a-1≥0
≤1且1-a-1≥0
