
分析 (1)根據平面向量的坐標表示與數量積運算,即可求出$\overrightarrow a$、$\overrightarrow b$的夾角余弦值;
(2)根據兩向量垂直,數量積為0,列出方程求出λ的值.
解答 解:(1)向量$\overrightarrow a=(4,3)$,$\overrightarrow b=(1,2)$,則
$\overrightarrow{a}$•$\overrightarrow{b}$=4×1+3×2=10,
且|$\overrightarrow{a}$|=$\sqrt{{4}^{2}{+3}^{2}}$=5,
|$\overrightarrow{b}$|=$\sqrt{{1}^{2}{+2}^{2}}$=$\sqrt{5}$;
設$\overrightarrow a$與$\overrightarrow b$的夾角為θ,則
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{10}{5×\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$;
(2)若$\overrightarrow a-λ\overrightarrow b$與$2\overrightarrow a+\overrightarrow b$垂直,
則($\overrightarrow{a}$-λ$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=0,
即2${\overrightarrow{a}}^{2}$+(1-2λ)$\overrightarrow{a}$•$\overrightarrow{b}$-λ${\overrightarrow{b}}^{2}$=0,
所以2×52+10(1-2λ)-5λ=0,
解得λ=$\frac{12}{5}$.
點評 本題考查了平面向量的坐標表示與數量積運算問題,是基礎題目.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若A,B,C是平面內的三點,則$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$ | |
| B. | 若$\overrightarrow{e_1}、\overrightarrow{e_2}$是兩個單位向量,則$\overrightarrow{e_1}=\overrightarrow{e_2}$ | |
| C. | 若$\overrightarrow a、\overrightarrow b$是任意兩個向量,則$|{\overrightarrow a+\overrightarrow b}|≤|{\overrightarrow a}|+|{\overrightarrow b}|$ | |
| D. | 向量$\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(1,-2)$可以作為平面內所有向量的一組基底 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
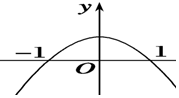 已知f′(x)是f(x)的導數,且y=xf′(x)的圖象如圖所示,則下列關于f(x)說法正確的是( )
已知f′(x)是f(x)的導數,且y=xf′(x)的圖象如圖所示,則下列關于f(x)說法正確的是( )| A. | 在(-∞,0)上是增函數 | B. | 在(-1,1)上是增函數 | ||
| C. | 在(-1,0)上是增函數 | D. | 在(1,+∞)上是減函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com