
���}Ŀ����D��ʾ�������F![]() �ĵ�����߅�L(zh��ng)��2�������Σ�ƽ��
�ĵ�����߅�L(zh��ng)��2�������Σ�ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��
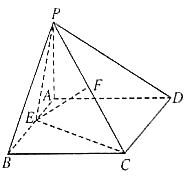
��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2���O(sh��)![]() ��
��![]() �����c(di��n)����߅
�����c(di��n)����߅![]() ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)![]() ��ʹ
��ʹ![]() ƽ��
ƽ��![]() ������˕r(sh��)�c(di��n)
������˕r(sh��)�c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x��
�ľ��x��
���𰸡���1���C��Ҋ��������2��![]() .
.
��������
��1����ƽ��![]() ƽ��
ƽ��![]() �ó�
�ó�![]() ƽ��
ƽ��![]() ��
��![]() ���Ķ��C��
���Ķ��C��![]() ƽ��
ƽ��![]() ���ɵ�ƽ��
���ɵ�ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����(d��ng)![]() ��
��![]() �����c(di��n)�r(sh��)��
�����c(di��n)�r(sh��)��![]() ƽ��
ƽ��![]() ������(j��)�}��ֱ���cƽ��ƽ�е��ж����������C���������õȷe������c(di��n)
������(j��)�}��ֱ���cƽ��ƽ�е��ж����������C���������õȷe������c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x�����ɵó��c(di��n)
�ľ��x�����ɵó��c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x��
�ľ��x��
��1���C����ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��
��![]() ƽ��
ƽ��![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
��?y��n)?/span>![]() ƽ��
ƽ��![]()
![]() ��
��
��![]() ��
��
��?y��n)?/span>![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]()
![]() ƽ��
ƽ��![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��
![]() ƽ��
ƽ��![]() ƽ��
ƽ��![]() ��
��
��2���⣺��(d��ng)![]() ��
��![]() �����c(di��n)�r(sh��)��
�����c(di��n)�r(sh��)��![]() ƽ��
ƽ��![]() ��
��
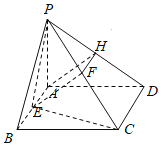
�C�����£��O(sh��)![]() �����c(di��n)��
�����c(di��n)��![]() ���B��
���B��![]() ��
��![]() ��
��
![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]() ����
����![]() ��
��
![]() ��߅��
��߅��![]() ��ƽ����߅�Σ�
��ƽ����߅�Σ�
![]() ����
����![]() ƽ��
ƽ��![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
�O(sh��)�c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x��
�ľ��x��![]() ��
��
�t![]() ��
��
���![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
![]() �c(di��n)
�c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x��
�ľ��x��![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������_(t��i)![]() �У�
�У�![]() ��G��H�քe��
��G��H�քe��![]() ��
��![]() �ϵ��c(di��n)��ƽ��
�ϵ��c(di��n)��ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() .
.
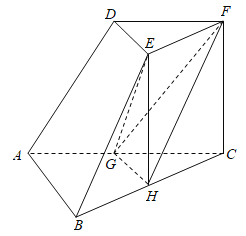
��1���C����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��
��![]() ��������
��������![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)�ֱ��l�^���タC��y2��4x�Ľ��c(di��n)F�����c���タC����M��N���c(di��n)�����c(di��n)M��x�S�Ϸ���
��1��������MN�Ĵ�ֱƽ�־���x�S���c(di��n)Q����|FQ|��8����ֱ��l��б�ʣ�
��2���O(sh��)�c(di��n)P��x0��0�������c(di��n)M������FP��ֱ���ĈA�⣬��x0��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ij��ij��1����15�յ���ƽ���ض�׃�����۾��D������(j��)ԓ�۾��D�����нY(ji��)Փ���_���ǣ�������
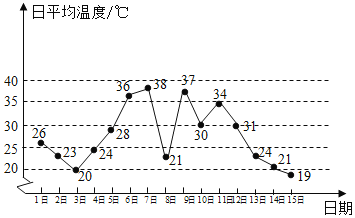
A. �@15����ƽ���ضȵĘO���![]()
B. �B�m(x��)������ƽ���ضȵķ���������7�գ�8�գ�9������
C. ���۾��D���A(y��)�y(c��)16�՜ض�Ҫ����![]()
D. ���۾��D���A(y��)�y(c��)���ض�С��![]() ���씵(sh��)���ڜضȴ���
���씵(sh��)���ڜضȴ���![]() ���씵(sh��)
���씵(sh��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����\(y��n)��(d��ng)�������vӍ�_�l(f��)��һ��(g��)���Ӌ(j��)����(sh��)��(j��)��(k��)�Ĺ����~̖(h��o)���Ñ�����ͨ�^�P(gu��n)ע���\(y��n)��(d��ng)����̖(h��o)�鿴�Լ�ÿ�����ߵIJ���(sh��)��ͬ�r(sh��)Ҳ���Ժ������Ñ��M(j��n)���\(y��n)��(d��ng)����![]() ���c(di��n)ٝ�����\(y��n)��(d��ng)����̖(h��o)���˽��Ñ���һЩ��r�������\(y��n)��(d��ng)�Ñ����S�C(j��)��ȡ��100���Ñ����y(t��ng)Ӌ(j��)������ijһ��IJ���(sh��)����(sh��)��(j��)�������£�
���c(di��n)ٝ�����\(y��n)��(d��ng)����̖(h��o)���˽��Ñ���һЩ��r�������\(y��n)��(d��ng)�Ñ����S�C(j��)��ȡ��100���Ñ����y(t��ng)Ӌ(j��)������ijһ��IJ���(sh��)����(sh��)��(j��)�������£�
|
|
|
|
|
|
|
| 5 | 20 | 50 | 15 | 5 | 5 |
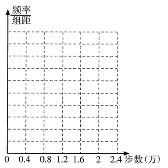
��1������(j��)���Д�(sh��)��(j��)������D��ʾ������(bi��o)ƽ�����������l�ʷֲ�ֱ���D�����ڿv�S�Ϙ�(bi��o)����С�L(zh��ng)���εĸߣ�
��2�����÷ӳ�ӵķ������IJ���(sh��)��![]() ���f�����г�ȡ7�ˣ���?g��u)��@7�����S�C(j��)��ȡ2�ˣ���(sh��)��
���f�����г�ȡ7�ˣ���?g��u)��@7�����S�C(j��)��ȡ2�ˣ���(sh��)��![]() ���f��������ǡ��1�˵ĸ��ʣ�
���f��������ǡ��1�˵ĸ��ʣ�
��3���@100���Ñ��У�![]() ���Ñ����������@Щ�����IJ���(sh��)���^1.2�f�����˞�20�ˣ��Ƿ���
���Ñ����������@Щ�����IJ���(sh��)���^1.2�f�����˞�20�ˣ��Ƿ���![]() �İ����J(r��n)���\(y��n)��(d��ng)����(sh��)���^1.2�f���c�Ԅe���P(gu��n)��
�İ����J(r��n)���\(y��n)��(d��ng)����(sh��)���^1.2�f���c�Ԅe���P(gu��n)��
����
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij��ӰƬ��ӯ���~����ӰƬ��Ʊ�������c�̶��ɱ�֮�ӛ��![]() ,�^Ӱ�˔�(sh��)ӛ��
,�^Ӱ�˔�(sh��)ӛ��![]() ,�亯��(sh��)�D����D��1����ʾ.����ĿǰԓƬӯ��δ�_(d��)���A(y��)��,���P(gu��n)�ˆT����˃ɷN�{(di��o)������,�D��2�����D��3���еČ�(sh��)���քe���{(di��o)����
,�亯��(sh��)�D����D��1����ʾ.����ĿǰԓƬӯ��δ�_(d��)���A(y��)��,���P(gu��n)�ˆT����˃ɷN�{(di��o)������,�D��2�����D��3���еČ�(sh��)���քe���{(di��o)����![]() �c
�c![]() ���(sh��)�D��.
���(sh��)�D��.

�o�������ķN�f��:
�وD��2����(du��)��(y��ng)�ķ�����:���Ʊ�r(ji��),����߳ɱ�;
�ڈD��2����(du��)��(y��ng)�ķ�����:����Ʊ�r(ji��)��׃,�����ͳɱ�;
�ۈD��3����(du��)��(y��ng)�ķ�����:���Ʊ�r(ji��),�����ֳɱ���׃;
�܈D��3����(du��)��(y��ng)�ķ�����:���Ʊ�r(ji��),�����ͳɱ�.
����,���_���f����____________.����������_�f���ľ�̖(h��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D1������߅��![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() .��
.��![]() ����
����![]() ������
������![]() ��λ�ã�
��λ�ã�![]() ƽ��
ƽ��![]() ���B�Y(ji��)
���B�Y(ji��)![]() ����D2.
����D2.
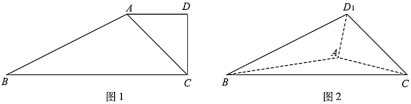
��1����(d��ng)![]() �r(sh��)���C����ƽ��
�r(sh��)���C����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����(d��ng)�����F![]() ���w�e���r(sh��)�����c(di��n)
���w�e���r(sh��)�����c(di��n)![]() ��ƽ��
��ƽ��![]() �ľ��x.
�ľ��x.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪![]() ������(bi��o)ԭ�c(di��n)���E�A
������(bi��o)ԭ�c(di��n)���E�A![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ���^
���^![]() ��ֱ��
��ֱ��![]() �c
�c![]() �ཻ��
�ཻ��![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() �M��
�M��![]() .
.
��1����(d��ng)![]() �ăAб�Ǟ�
�ăAб�Ǟ�![]() �r(sh��)����ֱ��
�r(sh��)����ֱ��![]() �ķ��̣�
�ķ��̣�
��2��ԇ̽����![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ�������ڣ�����c(di��n)
�鶨ֵ�������ڣ�����c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f������.
������(bi��o)���������ڣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
(1)������![]() ���c(di��n)
���c(di��n)![]() ̎���о����̣�
̎���о����̣�
(2)�C����![]() �څ^(q��)�g
�څ^(q��)�g![]() �����҃H��
�����҃H��![]() ��(g��)���c(di��n).
��(g��)���c(di��n).
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com