
【題目】正項等比數列{an},若2a1+3a2=1,a32=9a2a6 .
(1)求數列{an}的通項公式;
(2)設bn=log3a1+log3a2+log3a3+…log3an , 求數列{ ![]() }的前n項和Sn .
}的前n項和Sn .
【答案】
(1)解:依題意,a32=9a2a6=9a3a5,
∴ ![]() =q2=
=q2= ![]() ,
,
解得:q= ![]() 或q=﹣
或q=﹣ ![]() (舍),
(舍),
又∵2a1+3a2=1,即2a1+3 ![]() a1=1,
a1=1,
∴a1= ![]() ,
,
∴數列{an}是首項、公比均為 ![]() 的等比數列,
的等比數列,
∴其通項公式an= ![]()
(2)解:由(1)可知log3an=log3 ![]() =﹣n,
=﹣n,
∴bn=log3a1+log3a2+log3a3+…log3an
=﹣1﹣2﹣…﹣n
=﹣ ![]() ,
,
∴ ![]() =﹣
=﹣ ![]() =﹣2(
=﹣2( ![]() ﹣
﹣ ![]() ),
),
∴數列{ ![]() }的前n項和Sn=﹣2(1﹣
}的前n項和Sn=﹣2(1﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
=﹣2(1﹣ ![]() )
)
=﹣ ![]() .
.
【解析】(1)通過a32=9a2a6=9a3a5計算可知 ![]() =q2=
=q2= ![]() ,進而可知公比q=
,進而可知公比q= ![]() ,通過2a1+3a2=1可知a1=
,通過2a1+3a2=1可知a1= ![]() ,進而計算可得結論;(2)通過(1)可知log3an=﹣n,從而bn=﹣
,進而計算可得結論;(2)通過(1)可知log3an=﹣n,從而bn=﹣ ![]() ,裂項可知
,裂項可知 ![]() =﹣2(
=﹣2( ![]() ﹣
﹣ ![]() ),并項相加即得結論.
),并項相加即得結論.
【考點精析】解答此題的關鍵在于理解等比數列的通項公式(及其變式)的相關知識,掌握通項公式:![]() ,以及對數列的前n項和的理解,了解數列{an}的前n項和sn與通項an的關系
,以及對數列的前n項和的理解,了解數列{an}的前n項和sn與通項an的關系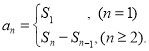 .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】數列![]() 中,
中,![]() 在直線
在直線![]() .
.
(1)求數列{an}的通項公式;
(2)令![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() .
.
(ⅰ)求![]() ;
;
(ⅱ)是否存在整數λ![]() ,使得不等式(-1)nλ<
,使得不等式(-1)nλ<![]() (n∈N
(n∈N![]() )恒成立?若存在,求出λ的取值的集合;若不存在,請說明理由.
)恒成立?若存在,求出λ的取值的集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100 個網箱,測量各箱水產品的產量(單位:kg),其頻率分布直方圖如圖:
(Ⅰ)設兩種養殖方法的箱產量相互獨立,記A表示事件“舊養殖法的箱產量低于50kg,新養殖法的箱產量不低于50kg”,估計A的概率;
(Ⅱ)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關:
箱產量<50kg | 箱產量≥50kg | |
舊養殖法 | ||
新養殖法 |
(Ⅲ)根據箱產量的頻率分布直方圖,求新養殖法箱產量的中位數的估計值(精確到0.01).
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sin(ωx﹣
sin(ωx﹣ ![]() )+b(ω>0),且函數圖象的對稱中心到對稱軸的最小距離為
)+b(ω>0),且函數圖象的對稱中心到對稱軸的最小距離為 ![]() ,當x∈[0,
,當x∈[0, ![]() ]時,f(x)的最大值為1.
]時,f(x)的最大值為1.
(1)求函數f(x)的解析式;
(2)將函數f(x)的圖象向右平移 ![]() 個單位長度得到函數g(x)圖象,若g(x)﹣3≤m≤g(x)+3在x∈[0,
個單位長度得到函數g(x)圖象,若g(x)﹣3≤m≤g(x)+3在x∈[0, ![]() ]上恒成立,求實數m的取值范圍.
]上恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊是a,b,c,已知2b﹣c=2acosC.
(1)求A;
(2)若4(b+c)=3bc,a=2 ![]() ,求△ABC的面積S.
,求△ABC的面積S.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分別拋擲兩顆骰子各一次,觀察向上的點數,求:
(1)兩數之和為5的概率;
(2)以第一次向上的點數為橫坐標![]() ,第二次向上的點數為縱坐標
,第二次向上的點數為縱坐標![]() 的點
的點![]() 在圓
在圓![]() 內部的概率.
內部的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣1|+|x﹣a|.
(1)若a=2,解不等式f(x)≥2;
(2)若a>1,x∈R,f(x)+|x﹣1|≥1,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x∈(1,+∞),函數f(x)=ex+2ax(a∈R),函數g(x)=| ![]() ﹣lnx|+lnx,其中e為自然對數的底數.
﹣lnx|+lnx,其中e為自然對數的底數.
(1)若a=﹣ ![]() ,求函數f(x)的單調區間;
,求函數f(x)的單調區間;
(2)證明:當a∈(2,+∞)時,f′(x﹣1)>g(x)+a.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com