
分析 利用二次函數與對數函數的單調性可求得當x1,x2∈[1,4]時,f(x1)min=2,g(x2)max=2+m,依題意,f(x1)min≥g(x2)max,解之即可求得實數m的取值范圍.
解答 解:∵f(x)=x2-2x+3的開口方向向上,對稱軸方程為:x=1,
∴當x1∈[1,4]時,f(x1)min=f(1)=2;
又g(x)=log2x+m為增函數,
∴當x2∈[1,4]時,g(x2)max=log24+m=2+m,
∵?x1,x2∈[1,4],有f(x1)≥g(x2)成立,
∴f(x1)min≥g(x2)max,即2≥2+m,
解得:m≤0.
故答案為:(-∞,0].
點評 本題考查函數恒成立問題,考查二次函數與對數函數的單調性與閉區間上的最值的求法,分析得到f(x1)min≥g(x2)max是關鍵,考查推理與運算能力,屬于中檔題.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數 | B. | 偶函數 | ||
| C. | 既不是奇函數又不是偶函數 | D. | 既是奇函數又是偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
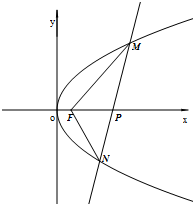 已知曲線C上任意一點到點F(1,0)的距離比到直線x+2=0的距離小1,點P(4,0).
已知曲線C上任意一點到點F(1,0)的距離比到直線x+2=0的距離小1,點P(4,0).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,2) | B. | (0,2] | C. | [0,2) | D. | [-2,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com