【題目】為了增強學(xué)生的環(huán)境意識，某中學(xué)隨機抽取了50名學(xué)生舉行了一次環(huán)保知識競賽，本次競賽的成績（得分均為整數(shù)，滿分100分）整理，制成下表：
成績 |
|
|
|
|
|
|
頻數(shù) | 2 | 3 | 14 | 15 | 14 | 4 |
（1）作出被抽查學(xué)生成績的頻率分布直方圖；
（2）若從成績在
中選一名學(xué)生，從成績在
中選出2名學(xué)生，共3名學(xué)生召開座談會，求組中學(xué)生
和組中學(xué)生
同時被選中的概率？
天天向上一本好卷系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知在極坐標系中曲線C的極坐標方程為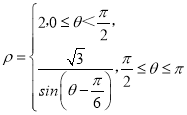
．
（1）求曲線C與極軸所在直線圍成圖形的面積；
（2）設(shè)曲線C與曲線ρsinθ＝1交于A，B，求|AB|．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
．
（1）討論
時，
的單調(diào)性、極值；
（2）求證：在(1)的條件下，
；
（3）是否存在實數(shù)a，使的最小值是3，如果存在，求出a的值；若不存在，
請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在一次比賽中，某隊的六名隊員均獲得獎牌，共獲得4枚金牌2枚銀牌，在頒獎晚會上，這六名隊員與1名領(lǐng)隊排成一排合影，若兩名銀牌獲得者需站在領(lǐng)隊的同側(cè)，則不同的排法共有______種．（用數(shù)字作答）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知F(0,1)為平面上一點，H為直線l：y=﹣1上任意一點，過點H作直線l的垂線m，設(shè)線段FH的中垂線與直線m交于點P，記點P的軌跡為Γ.
（1）求軌跡Γ的方程；
（2）過點F作互相垂直的直線AB與CD，其中直線AB與軌跡Γ交于點AB，直線CD與軌跡Γ交于點CD，設(shè)點M，N分別是AB和CD的中點.
①問直線MN是否恒過定點，如果經(jīng)過定點，求出該定點，否則說明理由；
②求△FMN的面積的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數(shù)方程為
（其中
為參數(shù)），以原點
為極點，以
軸非負半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（Ⅰ）求曲線的普通方程與曲線的直角坐標方程；
（Ⅱ）設(shè)點
，
分別是曲線，上兩動點且
，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在四棱柱
中，底面
是等腰梯形，
，頂點
在底面內(nèi)的射影恰為點
．
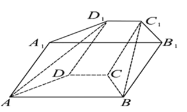
（1）求證：
平面
；
（2）若直線
與底面所成的角為
，求平面
與平面所成銳二面角的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標系
中，已知圓
：
，點
，
，點
在圓上，
.
（1）求圓的方程；
（2）直線
與圓交于
，
兩點（點在
軸上方），點
是拋物線
上的動點，點
為
的外心，求線段
長度的最大值，并求出當線段長度最大時，外接圓的標準方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】國際上通常用年齡中位數(shù)指標作為劃分國家或地區(qū)人口年齡構(gòu)成的標準：年齡中位數(shù)在20歲以下為“年輕型”人口；年齡中位數(shù)在20～30歲為“成年型”人口；年齡中位數(shù)在30歲以上為“老齡型”人口．
如圖反映了我國全面放開二孩政策對我國人口年齡中位數(shù)的影響．據(jù)此，對我國人口年齡構(gòu)成的類型做出如下判斷：①建國以來直至2000年為“成年型”人口；②從2010年至2020年為“老齡型”人口；③放開二孩政策之后我國仍為“老齡型”人口．其中正確的是（ ）
A.②③B.①③C.②D.①②
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
