四邊形ABCD中
＝2
，則四邊形ABCD為
A．平行四邊形
B．矩形
C．梯形
D．菱形
科目：高中數學 來源：101網校同步練習 高三數學 蘇教版(新課標·2004年初審) 蘇教版 題型：044
四邊形ABCD中
＝(6，1)，
＝(x，y)，
＝(－2，－3)，
(1)若
∥
，求x與y間的關系式；
(2)滿足(1)問的同時又有
⊥
，求x，y的值及四邊形ABCD的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
空間四邊形ABCD中，AB、BC、CD的中點分別為P、Q、R，且AC＝4，BD＝2
，PR＝3，則AC和BD所成的角為( )
A．90° B．60°
C．45° D．30°
查看答案和解析>>
科目：高中數學 來源：2012-2013學年山東省高三高考模擬卷（二）文科數學試卷（解析版） 題型：解答題
如圖，四邊形ABCD中，AB⊥AD，AD∥BC，AD＝6，BC＝4，AB＝2，E、F分別在BC、AD上，EF∥AB．現將四邊形ABEF沿EF折起，使得平面ABEF
平面EFDC．
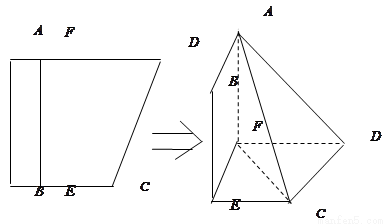
(Ⅰ) 當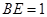
，是否在折疊后的AD上存在一點
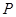，且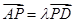
，使得CP∥平面ABEF？若存在，求出
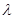的值；若不存在，說明理由；
(Ⅱ) 設BE＝x，問當x為何值時，三棱錐A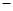
CDF的體積有最大值？并求出這個最大值．
查看答案和解析>>
科目：高中數學 來源：新課標高三數學直線、平面、簡單幾何體專項訓練（河北） 題型：解答題
如圖所示，四棱錐P－ABCD中，PD⊥平面ABCD，PA與平面ABCD所成的角為60°，在四邊形ABCD中，∠D＝∠DAB＝90°，AB＝4，CD＝1，AD＝2.
(1)建立適當的坐標系，并寫出點B，P的坐標；
(2)求異面直線PA與BC所成角的余弦值；
(3)若PB的中點為M，求證：平面AMC⊥平面PBC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
＝2
，∴
