
【題目】設函數![]() .
.
(1)試說明![]() 的圖象由函數
的圖象由函數![]() 的圖象經過怎樣的變化得到?并求
的圖象經過怎樣的變化得到?并求![]() 的單調區間;
的單調區間;
(2)若函數![]() 與
與![]() 的圖象關于直線
的圖象關于直線![]() 對稱,當
對稱,當![]() 時,求函數
時,求函數![]() 的最值.
的最值.
【答案】(1)見解析(2)最小值為﹣1;最大值為![]()
【解析】試題分析:(1)利用三角恒等變換化簡![]() 的解析式,再利用函數
的解析式,再利用函數![]() 的圖象變換規律,得出結論.
的圖象變換規律,得出結論.
(2)先根據對稱性求得![]() 的解析式,再利用正弦函數的定義域和值域,求得當
的解析式,再利用正弦函數的定義域和值域,求得當![]() ]時,函數
]時,函數![]() 的最值.
的最值.
試題解析:(1)∵函數![]() =sin
=sin![]() xcos
xcos![]() ﹣cos
﹣cos![]() xsin
xsin![]() ﹣cos
﹣cos![]() x﹣1=
x﹣1=![]() sin
sin![]() x﹣
x﹣![]() cos
cos![]() ﹣1=
﹣1=![]() sin(
sin(![]() x﹣
x﹣![]() )﹣1,
)﹣1,
故把函數![]() 的圖象向右平移1個單位,可得y=
的圖象向右平移1個單位,可得y=![]() sin(
sin(![]() x﹣
x﹣![]() )的圖象;
)的圖象;
再向下平移1個單位,可得f(x)的圖象.
(2)函數y=g(x)與y=f(x)的圖象關于直線x=2對稱,∴g(x)=f(4﹣x)=![]() sin[
sin[![]() (4﹣x)﹣
(4﹣x)﹣![]() ]﹣1=sin(
]﹣1=sin(![]() x)﹣1,
x)﹣1,
當x∈[0,1]時,![]() x∈[0,
x∈[0,![]() ],故當x=0時,函數y=g(x)取得最小值為﹣1;當x=1時,函數y=g(x)取得最大值為
],故當x=0時,函數y=g(x)取得最小值為﹣1;當x=1時,函數y=g(x)取得最大值為![]() ﹣1.
﹣1.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,長方體ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,點E,F分別在A1B1 , D1C1上,A1E=D1F=4.過E,F的平面α與此長方體的面相交,交線圍成一個正方形 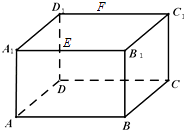
(1)在圖中畫出這個正方形(不必說出畫法和理由)
(2)求平面α把該長方體分成的兩部分體積的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區2008年至2016年糧食產量的部分數據如下表:

(1)求該地區2008年至2016年的糧食年產量![]() 與年份
與年份![]() 之間的線性回歸方程;
之間的線性回歸方程;
(2)利用(1)中的回歸方程,分析2008年至2016年該地區糧食產量的變化情況,并預測該地區 2018年的糧食產量.
附:回歸直線的斜率和截距的最小二乘估計公式分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,M、N分別是棱AA1、AD的中點,設E是棱AB的中點. 
(1)求證:MN∥平面CEC1;
(2)求平面D1EC1與平面ABCD所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將參加數學競賽的1000名學生編號如下:0001,0002,003,…,1000,打算從中抽取一個容量為50的樣本,按系統抽樣的方法把編號分成50個部分,如果第一部分編號為0001,0002,0003,…,0020,第一部分隨機抽取一個號碼為0013,那么抽取的第40個號碼 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com