
【題目】下列說法正確的有_________.
①函數(shù)![]() 的一個對稱中心為
的一個對稱中心為![]() ;
;
②在![]() 中,
中, ![]() 是
是![]() 的中點(diǎn),則
的中點(diǎn),則![]() ;
;
③在![]() 中,
中, ![]() 是
是![]() 的充要條件;
的充要條件;
④定義![]() ,已知
,已知![]() ,則
,則![]() 的最大值為
的最大值為![]() .
.
【答案】①②③④
【解析】 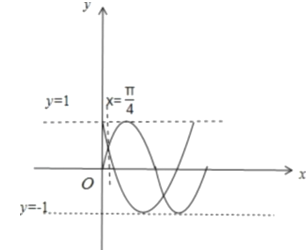
①對于函數(shù)![]() ,令
,令![]() ,求得
,求得![]() ,故函數(shù)
,故函數(shù)![]() 的圖象的一個對稱中心為
的圖象的一個對稱中心為![]() ,故①正確;②在
,故①正確;②在![]() 中,
中, ![]() 是
是![]() 的中點(diǎn),則
的中點(diǎn),則![]() ,故②正確;③在
,故②正確;③在![]() 中,
中, ![]() ,等價于
,等價于![]() ,等價于
,等價于![]() ,等價于
,等價于![]() ,等價于
,等價于![]() ,等價于
,等價于![]() ,故③正確;④定義
,故③正確;④定義![]() ,已知
,已知![]() ,畫出
,畫出![]() 和
和![]() 的圖象,如圖所示,則由圖可知,當(dāng)
的圖象,如圖所示,則由圖可知,當(dāng)![]() 時,
時, ![]() 取得最大值為
取得最大值為![]() ,故④正確,故答案為①②③④.
,故④正確,故答案為①②③④.
【 方法點(diǎn)睛】本題主要通過對多個命題真假的判斷,主要綜合考查向量的線性運(yùn)算及三角函數(shù)的圖象與性質(zhì),屬于難題.這種題型綜合性較強(qiáng),也是高考的命題熱點(diǎn),同學(xué)們往往因?yàn)槟骋惶幹R點(diǎn)掌握不好而導(dǎo)致“全盤皆輸”,因此做這類題目更要細(xì)心、多讀題,盡量挖掘出題目中的隱含條件,另外,要注意從簡單的自己已經(jīng)掌握的知識點(diǎn)入手,然后集中精力突破較難的命題.


 期末好成績系列答案
期末好成績系列答案 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百強(qiáng)名校期末沖刺100分系列答案
百強(qiáng)名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著人們對環(huán)境關(guān)注度的提高,綠色低碳出行越來越受到市民重視. 為此貴陽市建立了公共自行車服務(wù)系統(tǒng),市民憑本人二代身份證到自行車服務(wù)中心辦理誠信借車卡借車,初次辦卡時卡內(nèi)預(yù)先贈送20積分,當(dāng)積分為0時,借車卡將自動鎖定,限制借車,用戶應(yīng)持卡到公共自行車服務(wù)中心以1元購1個積分的形式再次激活該卡,為了鼓勵市民租用公共自行車出行,同時督促市民盡快還車,方便更多的市民使用,公共自行車按每車每次的租用時間進(jìn)行扣分收費(fèi),具體扣分標(biāo)準(zhǔn)如下:
①租用時間不超過1小時,免費(fèi);
②租用時間為1小時以上且不超過2小時,扣1分;
③租用時間為2小時以上且不超過3小時,扣2分;
④租用時間超過3小時,按每小時扣2分收費(fèi)(不足1小時的部分按1小時計(jì)算).
甲、乙兩人獨(dú)立出行,各租用公共自行車一次,兩人租車時間都不會超過3小時,設(shè)甲、乙租用時間不超過1小時的概率分別是0.4和0.5;租用時間為1小時以上且不超過2小時的概率分別是0.4和0.3.
(1)求甲、乙兩人所扣積分相同的概率;
(2)設(shè)甲、乙兩人所扣積分之和為隨機(jī)變量![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)試說明![]() 的圖象由函數(shù)
的圖象由函數(shù)![]() 的圖象經(jīng)過怎樣的變化得到?并求
的圖象經(jīng)過怎樣的變化得到?并求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 與
與![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱,當(dāng)
對稱,當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的最值.
的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)進(jìn)入某商場的每一位顧客購買甲種商品的概率為0.5,購買乙種商品的概率為0.6,且購買甲種商品與購買乙種商品相互獨(dú)立,各顧客之間購買商品也是相互獨(dú)立的.
(1)求進(jìn)入商場的1位顧客購買甲、乙兩種商品中的一種的概率;
(2)求進(jìn)入商場的1位顧客至少購買甲、乙兩種商品中的一種的概率;
(3)記ξ表示進(jìn)入商場的3位顧客中至少購買甲、乙兩種商品中的一種的人數(shù),求ξ的分布列及期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,(
,( ![]() 為參數(shù)).
為參數(shù)).
(1)將兩曲線化成普通坐標(biāo)方程;
(2)求兩曲線的公共弦長及公共弦所在的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】實(shí)數(shù)m取什么數(shù)值時,復(fù)數(shù)z=m2﹣1+(m2﹣m﹣2)i分別是:
(1)實(shí)數(shù)?
(2)虛數(shù)?
(3)純虛數(shù)?
(4)表示復(fù)數(shù)z的點(diǎn)在復(fù)平面的第四象限?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y=f(x)是定義域?yàn)镽的偶函數(shù),當(dāng)x≥0時,f(x)= 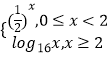 ,若關(guān)于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7個不同實(shí)數(shù)根,則a的取值范圍是 .
,若關(guān)于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7個不同實(shí)數(shù)根,則a的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,內(nèi)角A,B,C對邊的邊長分別是a,b,c,已知c=2,C= ![]() . (Ⅰ)若△ABC的面積等于
. (Ⅰ)若△ABC的面積等于 ![]() ,求a,b;
,求a,b;
(Ⅱ)若sinC+sin(B﹣A)=2sin2A,求△ABC的面積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com