
【題目】如圖,在平面直角坐標系![]() 中,設點
中,設點![]() 是橢圓
是橢圓![]() :
: ![]() 上一點,從原點
上一點,從原點![]() 向圓
向圓![]() :
: ![]() 作兩條切線分別與橢圓
作兩條切線分別與橢圓![]() 交于點
交于點![]() ,
, ![]() ,直線
,直線![]() ,
, ![]() 的斜率分別記為
的斜率分別記為![]() ,
, ![]() .
.

(1)求證: ![]() 為定值;
為定值;
(2)求四邊形![]() 面積的最大值.
面積的最大值.
【答案】(1)證明見解析;(2)1.
【解析】試題分析:(1)因為直線![]() :
: ![]() ,
, ![]() :
: ![]() ,與圓
,與圓![]() 相切,推出
相切,推出![]() ,
, ![]() 是方程
是方程![]() 的兩個不相等的實數根,利用韋達定理得
的兩個不相等的實數根,利用韋達定理得![]() ,結合點點
,結合點點![]() 在橢圓
在橢圓![]() 上,得出
上,得出![]() ;(2)當直線
;(2)當直線![]() ,
, ![]() 不落在坐標軸上時,設
不落在坐標軸上時,設![]() ,
, ![]() ,通過
,通過![]() ,推出
,推出![]() ,結合
,結合![]() ,
, ![]() 在橢圓
在橢圓![]() 上,可得
上,可得![]() ,再討論直線落在坐標軸上時,顯然有
,再討論直線落在坐標軸上時,顯然有![]() ,然后表示出
,然后表示出![]() ,結合基本不等式即可求出四邊形
,結合基本不等式即可求出四邊形![]() 面積的最大值.
面積的最大值.
試題解析:(1)因為直線![]() :
: ![]() ,
, ![]() :
: ![]() ,與圓
,與圓![]() 相切,
相切,
由 ,可得
,可得![]() ,
, ![]() 是方程
是方程![]() 的兩個不相等的實數根
的兩個不相等的實數根
∴![]() ,因為點
,因為點![]() 在橢圓
在橢圓![]() 上,所以
上,所以![]() ,
,
∴![]() .
.
(2)(i)當直線![]() ,
, ![]() 不落在坐標軸上時,設
不落在坐標軸上時,設![]() ,
, ![]() ,
,
因為![]() ,所以
,所以![]() ,即
,即![]() ,
,
因為![]() ,
, ![]() 在橢圓
在橢圓![]() 上,
上,
所以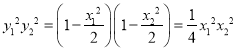 ,
,
整理得![]() ,所以
,所以![]() ,
,
所以![]() .
.
(ii)當直線落在坐標軸上時,顯然有![]() ,
,
綜上: ![]() .
.
因為![]() ,
,
因為![]() ,
,
所以![]() 的最大值為1.
的最大值為1.


科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,拋物線
為坐標原點,拋物線![]() 在第一象限內的點
在第一象限內的點![]() 到焦點的距離為
到焦點的距離為![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線交
處的切線交![]() 軸于點
軸于點![]() ,直線
,直線![]() 經過點
經過點![]() 且垂直于
且垂直于![]() 軸.
軸.
(Ⅰ)求線段![]() 的長;
的長;
(Ⅱ)設不經過點![]() 和
和![]() 的動直線
的動直線![]() 交曲線
交曲線![]() 于點
于點![]() 和
和![]() ,交
,交![]() 于點
于點![]() ,若直線
,若直線![]() 的斜率依次成等差數列,試問:
的斜率依次成等差數列,試問:![]() 是否過定點?請說明理由.
是否過定點?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點.
的中點.
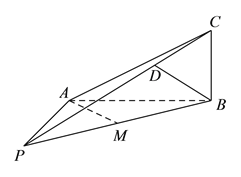
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】唐三彩,中國古代陶瓷燒制工藝的珍品,它吸取了中國國畫、雕塑等工藝美術的特點,在中國文化中占有重要的歷史地位,在陶瓷史上留下了濃墨重彩的一筆.唐三彩的生產至今已有1300多年的歷史,制作工藝十分復雜,它的制作過程必須先后經過兩次燒制,當第一次燒制合格后方可進入第二次燒制,兩次燒制過程相互獨立。某陶瓷廠準備仿制甲、乙、丙三件不同的唐三彩工藝品,根據該廠全面治污后的技術水平,經過第一次燒制后,甲、乙、丙三件工藝品合格的概率依次為![]() ,
, ![]() ,
, ![]() ,經過第二次燒制后,甲、乙、丙三件工藝品合格的概率依次為
,經過第二次燒制后,甲、乙、丙三件工藝品合格的概率依次為![]() ,
, ![]() ,
, ![]() .
.
(1)求第一次燒制后甲、乙、丙三件中恰有一件工藝品合格的概率;
(2)經過前后兩次燒制后,甲、乙、丙三件工藝品成為合格工藝品的件數為![]() ,求隨機變量
,求隨機變量![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分14分)如圖,已知橢圓![]() :
:![]() ,其左右焦點為
,其左右焦點為![]() 及
及![]() ,過點
,過點![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
,![]() 的中垂線與
的中垂線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() 兩點,且
兩點,且![]() 、
、![]() 、
、![]() 構成等差數列.
構成等差數列.

(1)求橢圓![]() 的方程;
的方程;
(2)記△![]() 的面積為
的面積為![]() ,△
,△![]() (
(![]() 為原點)的面積為
為原點)的面積為![]() .試問:是否存在直線
.試問:是否存在直線![]() ,使得
,使得![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一盒中裝有除顏色外其余均相同的12個小球,從中隨機取出1個球,取出紅球的概率為![]() ,取出黑球的概率為
,取出黑球的概率為![]() ,取出白球的概率為
,取出白球的概率為![]() ,取出綠球的概率為
,取出綠球的概率為![]() .求:
.求:
(1)取出的1個球是紅球或黑球的概率;
(2)取出的1個球是紅球或黑球或白球的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com