【題目】如圖，在棱長為1的正方體
中，點P在線段
上運動，給出以下四個命題：
①異面直線
與
所成的角為定值；
②二面角
的大小為定值；
③三棱錐
的體積為定值；
其中真命題的個數為（ ）
A.0B.1C.2D.3
【答案】D
【解析】
對于①由題意及圖形利用異面直線所成角的概念及求異面直線間的方法及可求解；對于②由題意及平面具有延展性可知實質為平面
與平面
所成的二面角；對于③由題意及三棱錐的體積的算法中可以進行頂點可以輪換求解體積，和點P的位置及直線
與平面的位置即可判斷正誤．
解：對于①因為在棱長為1的正方體
中，
點P在線段上運動，有正方體的及題意易有
平面，
而
平面，所以
，
故這兩個異面直線所成的角為定值
，所以①正確；
對于②因為二面角
的大小，
實質為平面與平面所成的二面角而這兩的平面為固定的不變的平面所以夾角也為定值，故②正確；
對于③三棱錐
的體積還等于三棱錐的體積
的體積，
而平面
為固定平面且大小一定，又因為
，而
平面，
所以點A到平面DBC1的距離即為點P到該平面的距離，
所以三棱錐的體積為定值，故③正確．
故選：D．
時刻準備著暑假作業原子能出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目：高中數學 來源： 題型：
【題目】
如圖，在三棱錐P—ABC中，PC⊥底面ABC，AB⊥BC，D，E分別是AB，PB的中點．
（Ⅰ）求證：DE∥平面PAC．
（Ⅱ）求證：AB⊥PB；
（Ⅲ）若PC＝BC，求二面角P—AB—C的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
（
為參數），直線
的參數方程為
（
為參數）.
（Ⅰ）若
，求直線被曲線截得的線段的長度；
（Ⅱ）若
，在曲線上求一點
，使得點到直線的距離最小，并求出最小距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（Ⅰ）求過點A（2，6）且在兩坐標軸上的截距相等的直線m的方程；
（Ⅱ）求過點A（2，6）且被圓C：（x﹣3）2+（y﹣4）2＝4截得的弦長為
的直線l的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區某農產品近幾年的產量統計如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼t | 1 | 2 | 3 | 4 | 5 | 6 |
年產量y(萬噸) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（Ⅰ）根據表中數據，建立
關于的線性回歸方程
；
（Ⅱ）根據線性回歸方程預測2019年該地區該農產品的年產量.
附:對于一組數據
，其回歸直線的斜率和截距的最小二乘估計分別為：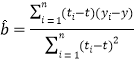
，
.(參考數據:
，計算結果保留小數點后兩位）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某居民區隨機抽取10個家庭，獲得第
個家庭的月收入
（單位：千元）與月儲蓄
（單位：千元）的數據資料，算得
， 
，
， 
(1).求家庭的月儲蓄
對月收入
的線性回歸方程
；
(2).判斷變量
與
之間的正相關還是負相關；
(3).若該居民區某家庭月收入為7千元，預測該家庭的月儲蓄.
附：回歸直線的斜率和截距的最小二乘估計公式分別為
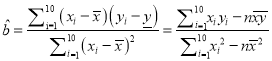
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出以下四個說法：
①殘差點分布的帶狀區域的寬度越窄相關指數越小
②在刻畫回歸模型的擬合效果時，相關指數
的值越大，說明擬合的效果越好；
③在回歸直線方程
中，當解釋變量
每增加一個單位時，預報變量
平均增加
個單位；
④對分類變量
與
，若它們的隨機變量
的觀測值
越小，則判斷“與有關系”的把握程度越大．
其中正確的說法是
A. ①④B. ②④C. ①③D. ②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
