
【題目】(Ⅰ)求過點A(2,6)且在兩坐標軸上的截距相等的直線m的方程;
(Ⅱ)求過點A(2,6)且被圓C:(x﹣3)2+(y﹣4)2=4截得的弦長為![]() 的直線l的方程.
的直線l的方程.
【答案】(Ⅰ)3x﹣y=0或x+y﹣8=0;(Ⅱ)x=2或3x+4y﹣30=0.
【解析】
(I)分成直線過原點和不過原點兩種情況,求得過![]() 且在兩坐標軸上的截距相等的直線方程.
且在兩坐標軸上的截距相等的直線方程.
(II)先根據弦長求得圓心到直線的距離.分成直線![]() 斜率不存在和存在兩種情況,求得直線
斜率不存在和存在兩種情況,求得直線![]() 的方程.
的方程.
(I)當直線l在兩坐標軸上的截距都等于0時,斜率k=3,直線l的方程為 y=3x;
當直線l在兩坐標軸上的截距不等于0時,
設直線l的方程 ![]() ,把點A(2,6)代入求得 a=8,
,把點A(2,6)代入求得 a=8,
故直線l的方程為![]() 即 x+y﹣8=0,
即 x+y﹣8=0,
故直線l的方程為3x﹣y=0或x+y﹣8=0;
(II)圓C:(x﹣3)2+(y﹣4)2=4的圓心C(3,4),半徑R=2,
∵直線l被圓C:(x﹣3)2+(y﹣4)2=4截得的弦長為![]() ,
,
故圓心C到直線l的距離d=1,
當直線l的斜率不存在時,直線x=2顯然滿足題意,
當直線l的斜率存在時,可設y﹣6=k(x﹣2),即kx﹣y+6﹣2k=0,
則d![]() 1,
1,
解可得,k![]() ,
,
此時直線l:3x+4y﹣30=0,
綜上可得直線l的方程x=2或3x+4y﹣30=0.


科目:高中數學 來源: 題型:
【題目】近年來,共享單車已經悄然進入了廣大市民的日常生活,并慢慢改變了人們的出行方式.為了更好地服務民眾,某共享單車公司在其官方![]() 中設置了用戶評價反饋系統,以了解用戶對車輛狀況和優惠活動的評價.現從評價系統中選出
中設置了用戶評價反饋系統,以了解用戶對車輛狀況和優惠活動的評價.現從評價系統中選出![]() 條較為詳細的評價信息進行統計,車輛狀況的優惠活動評價的
條較為詳細的評價信息進行統計,車輛狀況的優惠活動評價的![]() 列聯表如下:
列聯表如下:
對優惠活動好評 | 對優惠活動不滿意 | 合計 | |
對車輛狀況好評 |
|
|
|
對車輛狀況不滿意 |
|
|
|
合計 |
|
|
|
(1)能否在犯錯誤的概率不超過![]() 的前提下認為優惠活動好評與車輛狀況好評之間有關系?
的前提下認為優惠活動好評與車輛狀況好評之間有關系?
(2)為了回饋用戶,公司通過![]() 向用戶隨機派送騎行券.用戶可以將騎行券用于騎行付費,也可以通過
向用戶隨機派送騎行券.用戶可以將騎行券用于騎行付費,也可以通過![]() 轉贈給友.某用戶共獲得了
轉贈給友.某用戶共獲得了![]() 張騎行券,其中只有
張騎行券,其中只有![]() 張是一元券.現該用戶從這
張是一元券.現該用戶從這![]() 張騎行券中隨機選取
張騎行券中隨機選取![]() 張轉贈給好友,求選取的
張轉贈給好友,求選取的![]() 張中至少有
張中至少有![]() 張是一元券的概率.
張是一元券的概率.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為某兒童游樂場一個小型摩天輪示意圖,該摩天輪近似看作半徑為![]() 的圓,圓上最低點A與地面距離為
的圓,圓上最低點A與地面距離為![]() ,摩天輪每60秒勻速轉動一圈,摩天輪上某點B的起始位置在最低點A處.圖中
,摩天輪每60秒勻速轉動一圈,摩天輪上某點B的起始位置在最低點A處.圖中![]() 與地面垂直,以
與地面垂直,以![]() 為始邊,逆時針轉動
為始邊,逆時針轉動![]() 角到
角到![]() ,設B點與地面間的距離為
,設B點與地面間的距離為![]() .
.
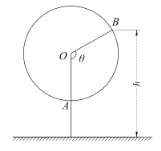
(1)求h與![]() 間關系的函數解析式;
間關系的函數解析式;
(2)設從![]() 開始轉動,經過t秒后到達
開始轉動,經過t秒后到達![]() ,求h與t之間的函數關系式;
,求h與t之間的函數關系式;
(3)如果離地面高度不低于![]() 才能獲得最佳觀景效果,在摩天輪轉動的一圈內,有多長時間B點在最佳觀景效果高度?
才能獲得最佳觀景效果,在摩天輪轉動的一圈內,有多長時間B點在最佳觀景效果高度?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為1的正方體![]() 中,點P在線段
中,點P在線段![]() 上運動,給出以下四個命題:
上運動,給出以下四個命題:

①異面直線![]() 與
與![]() 所成的角為定值;
所成的角為定值;
②二面角![]() 的大小為定值;
的大小為定值;
③三棱錐![]() 的體積為定值;
的體積為定值;
其中真命題的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知海島![]() 在海島
在海島![]() 北偏東
北偏東![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物體甲從海島
海里,物體甲從海島![]() 以
以![]() 海里/小時的速度沿直線向海島
海里/小時的速度沿直線向海島![]() 移動,同時物體乙從海島
移動,同時物體乙從海島![]() 沿著海島
沿著海島![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小時的速度移動.
海里/小時的速度移動.
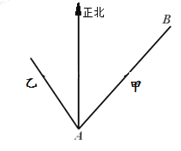
(1)問經過多長時間,物體甲在物體乙的正東方向;
(2)求甲從海島![]() 到達海島
到達海島![]() 的過程中,甲、乙兩物體的最短距離.
的過程中,甲、乙兩物體的最短距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我省5名醫學專家馳援湖北武漢抗擊新冠肺炎疫情現把專家全部分配到A,B,C三個集中醫療點,每個醫療點至少要分配1人,其中甲專家不去A醫療點,則不同分配種數為( )
A.116B.100C.124D.90
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com