
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(Ⅰ)若![]() ,求直線
,求直線![]() 被曲線
被曲線![]() 截得的線段的長度;
截得的線段的長度;
(Ⅱ)若![]() ,在曲線
,在曲線![]() 上求一點
上求一點![]() ,使得點
,使得點![]() 到直線
到直線![]() 的距離最小,并求出最小距離.
的距離最小,并求出最小距離.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
試題(Ⅰ)由題意,得曲線![]() 的普通方程和直線
的普通方程和直線![]() 的普通方程,聯立方程組,解焦點,即可求解截曲線
的普通方程,聯立方程組,解焦點,即可求解截曲線![]() 的線段長;
的線段長;
(Ⅱ)解法一:![]() 時,得直線
時,得直線![]() 的普通方程,由點到直線的距離公式,得到距離的表達式,轉化為三角函數的性質,即可求解最小值.
的普通方程,由點到直線的距離公式,得到距離的表達式,轉化為三角函數的性質,即可求解最小值.
試題解析:
(Ⅰ)曲線![]() 的普通方程為
的普通方程為![]() .
.
當![]() 時,直線
時,直線![]() 的普通方程為
的普通方程為![]() .
.
由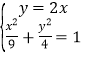 .解得
.解得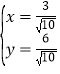 或
或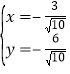 ,
,
直線![]() 被曲線
被曲線![]() 截得的線段的長度為
截得的線段的長度為![]() .
.
(Ⅱ)解法一:![]() 時,直線
時,直線![]() 的普通方程為
的普通方程為![]() .
.
由點到直線的距離公式,橢圓![]() 上的點
上的點![]() 到直線
到直線![]() :
:![]() 的距離為
的距離為
![]()
![]()
![]() ,
,
其中![]() 滿足
滿足![]() ,
,![]() .
.
由三角函數性質知,當![]() 時,
時,![]() 取最小值
取最小值![]() .
.
此時,![]() ,
,![]() .
.
因此,當點![]() 位于
位于![]() 時,點
時,點![]() 到
到![]() 的距離取最小值
的距離取最小值![]() .
.
解法二:當![]() 時,直線
時,直線![]() 的普通方程為
的普通方程為![]() .
.
設與![]() 平行,且與橢圓
平行,且與橢圓![]() 相切的直線
相切的直線![]() 的方程為
的方程為![]() .
.
由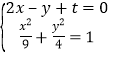 消去
消去![]() 并整理得
并整理得![]() .
.
由判別式![]() ,解得
,解得![]() .
.
所以,直線![]() 的方程為
的方程為![]() ,或
,或![]() .
.
要使兩平行直線![]() 與
與![]() 間的距離最小,則直線
間的距離最小,則直線![]() 的方程為
的方程為![]() .
.
這時,![]() 與
與![]() 間的距離
間的距離![]()
![]() .
.
此時點![]() 的坐標為方程組
的坐標為方程組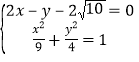 的解
的解 .
.
因此,當點![]() 位于
位于![]() 時,點
時,點![]() 到直線
到直線![]() 的距離取最小值
的距離取最小值![]() .
.


科目:高中數學 來源: 題型:
【題目】某工廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回歸直線方程![]() =bx+a;(其中
=bx+a;(其中 ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)預計在今后的銷售中,銷量與單價仍然服從(1)中的關系,且該產品的成本是4元/件,為使工廠獲得最大利潤,該產品的單價應定為多少元?(利潤=銷售收入-成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】5G網絡是第五代移動通信網絡,其峰值理論傳輸速度可達每8秒1GB,比4G網絡的傳輸速度快數百倍.舉例來說,一部1G的電影可在8秒之內下載完成.隨著5G技術的誕生,用智能終端分享3D電影、游戲以及超高畫質(UHD)節目的時代正向我們走來.某手機網絡研發公司成立一個專業技術研發團隊解決各種技術問題,其中有數學專業畢業,物理專業畢業,其它專業畢業的各類研發人員共計1200人.現在公司為提高研發水平,采用分層抽樣抽取400人按分數對工作成績進行考核,并整理得如上頻率分布直方圖(每組的頻率視為概率).

(1)從總體的1200名學生中隨機抽取1人,估計其分數小于50的概率;
(2)研發公司決定對達到某分數以上的研發人員進行獎勵,要求獎勵研發人員的人數達到30%,請你估計這個分數的值;
(3)已知樣本中有三分之二的數學專業畢業的研發人員分數不低于70分,樣本中不低于70分的數學專業畢業的研發人員人數與物理及其它專業畢業的研發人員的人數和相等,估計總體中數學專業畢業的研發人員的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,天津之眼,全稱天津永樂橋摩天輪,是世界上唯一一個橋上瞰景摩天輪,是天津的地標之一 .永樂橋分上下兩層,上層橋面預留了一個長方形開口,供摩天輪輪盤穿過,摩天輪的直徑為110米,外掛裝48個透明座艙,在電力的驅動下逆時針勻速旋轉,轉一圈大約需要30分鐘.現將某一個透明座艙視為摩天輪上的一個點![]() ,當點
,當點![]() 到達最高點時,距離下層橋面的高度為113米,點
到達最高點時,距離下層橋面的高度為113米,點![]() 在最低點處開始計時.
在最低點處開始計時.

(1)試確定在時刻![]() (單位:分鐘)時點
(單位:分鐘)時點![]() 距離下層橋面的高度
距離下層橋面的高度![]() (單位:米);
(單位:米);
(2)若轉動一周內某一個摩天輪透明座艙在上下兩層橋面之間的運行時間大約為5分鐘,問上層橋面距離下層橋面的高度約為多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為某兒童游樂場一個小型摩天輪示意圖,該摩天輪近似看作半徑為![]() 的圓,圓上最低點A與地面距離為
的圓,圓上最低點A與地面距離為![]() ,摩天輪每60秒勻速轉動一圈,摩天輪上某點B的起始位置在最低點A處.圖中
,摩天輪每60秒勻速轉動一圈,摩天輪上某點B的起始位置在最低點A處.圖中![]() 與地面垂直,以
與地面垂直,以![]() 為始邊,逆時針轉動
為始邊,逆時針轉動![]() 角到
角到![]() ,設B點與地面間的距離為
,設B點與地面間的距離為![]() .
.
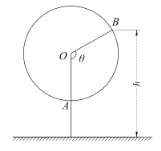
(1)求h與![]() 間關系的函數解析式;
間關系的函數解析式;
(2)設從![]() 開始轉動,經過t秒后到達
開始轉動,經過t秒后到達![]() ,求h與t之間的函數關系式;
,求h與t之間的函數關系式;
(3)如果離地面高度不低于![]() 才能獲得最佳觀景效果,在摩天輪轉動的一圈內,有多長時間B點在最佳觀景效果高度?
才能獲得最佳觀景效果,在摩天輪轉動的一圈內,有多長時間B點在最佳觀景效果高度?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司的電子新產品未上市時,原定每件售價100元,經過市場調研發現,該電子新產品市場潛力很大,該公司決定從第一周開始銷售時,該電子產品每件售價比原定售價每周漲價4元,5周后開始保持120元的價格平穩銷售,10周后由于市場競爭日益激烈,每周降價2元,直到15周結束,該產品不再銷售.
(Ⅰ)求售價![]() (單位:元)與周次
(單位:元)與周次![]() (
(![]() )之間的函數關系式;
)之間的函數關系式;
(Ⅱ)若此電子產品的單件成本![]() (單位:元)與周次
(單位:元)與周次![]() 之間的關系式為
之間的關系式為![]() ,
,![]() ,
,![]() ,試問:此電子產品第幾周的單件銷售利潤(銷售利潤
,試問:此電子產品第幾周的單件銷售利潤(銷售利潤![]() 售價
售價![]() 成本)最大?
成本)最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為1的正方體![]() 中,點P在線段
中,點P在線段![]() 上運動,給出以下四個命題:
上運動,給出以下四個命題:

①異面直線![]() 與
與![]() 所成的角為定值;
所成的角為定值;
②二面角![]() 的大小為定值;
的大小為定值;
③三棱錐![]() 的體積為定值;
的體積為定值;
其中真命題的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面四邊形![]() 中,
中, ![]() ,
, ![]() 為等邊三角形,現將
為等邊三角形,現將![]() 沿
沿![]() 翻折得到四面體
翻折得到四面體![]() ,點
,點![]() 分別為
分別為![]() 的中點.
的中點.


(Ⅰ)求證:四邊形![]() 為矩形;
為矩形;
(Ⅱ)當平面![]() 平面
平面![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通安全法有規定:機動車行經人行橫道時,應當減速行駛;遇行人正在通過人行橫道,應當停車讓行.機動車行經沒有交通信號的道路時,遇行人橫過馬路,應當避讓.我們將符合這條規定的稱為“禮讓斑馬線”,不符合這條規定的稱為“不禮讓斑馬線”.下表是六安市某十字路口監控設備所抓拍的5個月內駕駛員“不禮讓斑馬線”行為的統計數據:
月份 | 1 | 2 | 3 | 4 | 5 |
“不禮讓斑馬線”的駕駛員人數 | 120 | 105 | 100 | 85 | 90 |
(1)根據表中所給的5個月的數據,可用線性回歸模型擬合![]() 與
與![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)求“不禮讓斑馬線”的駕駛員人數![]() 關于月份
關于月份![]() 之間的線性回歸方程;
之間的線性回歸方程;
(3)若從4,5月份“不禮讓斑馬線”的駕駛員中分別選取4人和2人,再從所選取的6人中任意抽取2人進行交規調查,求抽取的2人分別來自兩個月份的概率;
參考公式:線性回歸方程![]() ,其中
,其中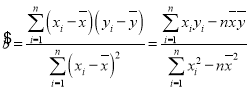 ,
,![]() ,
, .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com