①③④
分析:①根據偶函數定義可得g(-x)=f(-x)+f(x)=g(x),故①可判斷;
②若對任意x∈R都有f(x)+f(2-x)=0,可得f(x+2)=-f(-x),故②錯誤;
③由對任意x∈R都有f(x)+f(2+x)=0,可知f(2+x)=-f(x),根據f(x)是奇函數,可得f(-x)=-f(x),從而可判斷f(x)的圖象關于直線x=1對稱;
④利用函數單調性的定義,結合
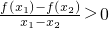
,可知函數f(x)為(-∞,+∞)上的增函數.
解答:①∵g(-x)=f(-x)+f(x)=g(x)
∴函數g(x)=f(x)+f(-x)一定是偶函數,故①正確;
②若對任意x∈R都有f(x)+f(2-x)=0,∴f(x)=-f(2-x),∴f(x+2)=-f(-x),f(x)不是以2為周期的周期函數,故②錯誤;
③∵對任意x∈R都有f(x)+f(2+x)=0,∴f(2+x)=-f(x)
∵f(x)是奇函數,∴f(-x)=-f(x)
∴f(2+x)=f(-x)
∴f(x)的圖象關于直線x=1對稱;
④設任意x
1,x
2∈R且x
1<x
2,∴x
1-x
2<0,
∵
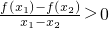
∴f(x
1)-f(x
2)<0
∴f(x
1)<f(x
2)
∴函數f(x)為(-∞,+∞)上的增函數.
點評:本題以函數為載體,主要考查函數的奇偶性,周期性,對稱性及函數的單調性,解題時應一一判斷.

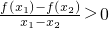 恒成立,則f(x)為(-∞,+∞)上的增函數.
恒成立,則f(x)為(-∞,+∞)上的增函數.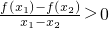 ,可知函數f(x)為(-∞,+∞)上的增函數.
,可知函數f(x)為(-∞,+∞)上的增函數.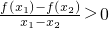


 備戰中考寒假系列答案
備戰中考寒假系列答案