
【題目】已知函數![]() ,
,![]() .
.
(1)若直線![]() 與曲線
與曲線![]() 和
和![]() 分別交于
分別交于![]() 兩點直線,且曲線
兩點直線,且曲線![]() 在
在![]() 處的切線與
處的切線與![]() 在
在![]() 處的切線相互平行,求正數
處的切線相互平行,求正數![]() 的最大值;
的最大值;
(2)若![]() 有三個不同的零點,求
有三個不同的零點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)問題可轉化為![]() 在
在![]() 有解,也就是
有解,也就是![]() 在
在![]() 有解,考慮
有解,考慮![]() 的圖像與直線
的圖像與直線![]() 有公共點即可得到參數
有公共點即可得到參數![]() 的最大值.
的最大值.
(2)因為![]() 有三個不同的零點,所以函數必有兩個不同的極值點,也就是導函數必有兩個不同的零點,從而
有三個不同的零點,所以函數必有兩個不同的極值點,也就是導函數必有兩個不同的零點,從而![]() .我們還需要論證當
.我們還需要論證當![]() ,
,![]() 確有三個不同的零點,這可以通過零點存在定理和單調性來判斷.
確有三個不同的零點,這可以通過零點存在定理和單調性來判斷.
詳解:(1)依題意,函數![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,![]() .
.
因為曲線![]() 在
在![]() 處的切線與
處的切線與![]() 在
在![]() 處的切線相互平行,
處的切線相互平行,
所以![]() 在
在![]() 有解,即方程
有解,即方程![]() 在
在![]() 有解.
有解.
方程![]() 在
在![]() 有解轉化為函數
有解轉化為函數![]() 與函數
與函數![]() 的圖象在
的圖象在![]() 上有交點.
上有交點.
令過原點且與函數![]() 的圖象相切的直線的斜率為
的圖象相切的直線的斜率為![]() ,只須
,只須![]() .
.
令切點為![]() ,則
,則![]() ,又
,又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
于是![]() ,所以
,所以![]() ,
,![]() 的最大值為
的最大值為![]()
(2)由題意![]() ,則
,則![]() ,
,
當![]() 時,∵
時,∵![]() ,
,
∴![]() 在
在![]() 上為增函數,不符合題意.
上為增函數,不符合題意.
當![]() 時,
時,![]() ,令
,令![]() ,則
,則
![]() .令
.令![]() 的兩根分別為
的兩根分別為![]() 且
且![]() ,
,
則∵![]() ,
,![]() ,∴
,∴![]() ,
,
當![]() 時,
時,![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上為增函數;
上為增函數;
當![]() 時,
時,![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上為減函數;
上為減函數;
當![]() 時,
時,![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上為增函數;
上為增函數;
∵![]() ,∴
,∴![]() 在
在![]() 上只有一個零點1,且
上只有一個零點1,且![]() ,
,![]() .
.
∴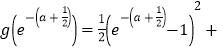
![]()
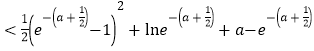
![]() .
.
∵![]() ,又當
,又當![]() 時,
時,![]() ,∴
,∴![]()
∴![]() 在
在![]() 上必有一個零點.
上必有一個零點.
∴![]()
![]()
![]() .
.
∵![]() ,又當
,又當![]() 時,
時,![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 上必有一個零點.
上必有一個零點.
綜上所述,故![]() 的取值范圍為
的取值范圍為![]() .
.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】已知:函數![]() ,當x∈(-3,2)時,
,當x∈(-3,2)時,![]() >0,當x∈(-
>0,當x∈(-![]() ,-3)
,-3)![]() (2,+
(2,+![]() )時,
)時,![]() <0
<0
(I)求a,b的值;
(II)若不等式![]() 的解集為R,求實數c的取值范圍.
的解集為R,求實數c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解用戶對其產品的滿意度,從A、B兩地區分別隨機調查了20個用戶,得到用戶對產品的滿意度評分如下:
A地區: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地區: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根據兩組數據完成兩地區用戶滿意度評分的莖葉圖,并通過莖葉圖比較兩地區滿意度的平均值及分散程度(不要求算出具體值,給出結論即可):

(Ⅱ)根據用戶滿意度評分,將用戶的滿意度從低到高分為三個等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
記事件C:“A地區用戶的滿意度等級高于B地區用戶的滿意度等級”,假設兩地區用戶的評價結果相互獨立,根據所給數據,以事件發生的頻率作為相應事件發生的概率,求C的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
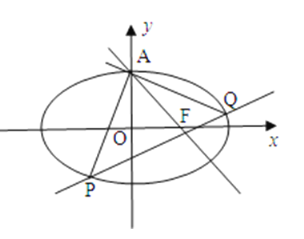
【題目】如圖,已知橢圓![]() 的上頂點為
的上頂點為![]() ,右焦點為
,右焦點為![]() ,直線
,直線![]() 與圓
與圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)不過點![]() 的動直線
的動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() .求證:直線
.求證:直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】耐鹽堿水稻俗稱“海水稻”,是一種可以長在灘涂和鹽堿地的水稻。還水稻的灌溉是將海水稀釋后進行灌溉。某實驗基礎為了研究海水濃度![]() (
(![]() )對畝產量
)對畝產量![]() (噸)的影響,通過在試驗田的種植實驗,測得了某種還水稻的畝產量與海水濃度的數據如下表:
(噸)的影響,通過在試驗田的種植實驗,測得了某種還水稻的畝產量與海水濃度的數據如下表:
海水濃度 |
|
|
|
|
|
畝產量 |
|
|
|
|
|
繪制散點圖發現,可用線性回歸模型擬合畝產量![]() 與海水濃度
與海水濃度![]() 之間的相關關系,用最小二乘法計算得
之間的相關關系,用最小二乘法計算得![]() 與
與![]() 之間的線性回歸方程為
之間的線性回歸方程為![]() .
.
(1)求出![]() 的值,并估算當澆灌海水濃度為8%時該品種的畝產量。
的值,并估算當澆灌海水濃度為8%時該品種的畝產量。
(2)①完成下列殘差表:
海水濃度 |
|
|
|
|
|
畝產量 |
|
|
|
|
|
| |||||
殘差 |
②統計學中常用相關指數![]() 來刻畫回歸效果,
來刻畫回歸效果,![]() 越大,模型擬合效果越好,如假設
越大,模型擬合效果越好,如假設![]() ,就說明預報變量
,就說明預報變量![]() 的差異有
的差異有![]() 是由解釋變量
是由解釋變量![]() 引起的.請計算相關指數
引起的.請計算相關指數![]() (精確到0.01),并指出畝產量的變化多大程度上是由澆灌海水濃度引起的.
(精確到0.01),并指出畝產量的變化多大程度上是由澆灌海水濃度引起的.
(附:殘差公式![]() ,相關指數
,相關指數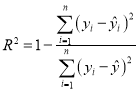 ,參考數據
,參考數據![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校對生源基地學校一年級的數學成績進行摸底調查,已知其中兩個摸底學校分別有![]() 人、
人、![]() 人,現采用分層抽樣的方法從兩個學校一共抽取了
人,現采用分層抽樣的方法從兩個學校一共抽取了![]() 名學生的數學成績,并作出了頻數分別統計表如下:(一年級人數為
名學生的數學成績,并作出了頻數分別統計表如下:(一年級人數為![]() 人的學校記為學校一,一年級人數為1000人的學校記為學校二)
人的學校記為學校一,一年級人數為1000人的學校記為學校二)
學校一
分組 |
|
|
|
|
頻道 |
|
|
|
|
分組 |
|
|
|
|
頻數 |
|
|
|
|
學校二
分組 |
|
|
|
|
頻道 |
|
|
|
|
分組 |
|
|
|
|
頻數 |
|
|
|
|
(1)計算![]() ,
,![]() 的值.
的值.
(2)若規定考試成績在![]() 內為優秀,請分別估計兩個學校數學成績的優秀率;
內為優秀,請分別估計兩個學校數學成績的優秀率;
(3)由以上統計數據填寫下面![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為兩個學校的數學成績有差異.
的把握認為兩個學校的數學成績有差異.
學校一 | 學校二 | 總計 | |
優秀 | |||
非優秀 | |||
總計 |
附:
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com