
分析 在①中,f(0+x)+f(0-x)=2,得a=0,b=1,滿足“準奇函數”的定義;在②中,根據函數“準奇函數”的定義,利用函數奇偶性的定義即可證明函數F(x)=f(x+a)-f(a)為R上的奇函數;在③中,f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,得點(1,2)為函數f(x)的“中心點”.
解答 解:在①中,∵函數f(x)=sinx+1,∴f(0+x)+f(0-x)=2,
∴a=0,b=1,滿足“準奇函數”的定義,故①正確;
在②中,若F(x)=f(x+a)-f(a),
則F(-x)+F(x)=f(x+a)-f(a)+f(-x+a)-f(a)=f(a-x)+f(a+x)-2f(a),
∵f(x)在R上的“中心點”為(a,f(a)),
∴f(a-x)+f(a+x)=2f(a),
即F(-x)+F(x)=f(a-x)+f(a+x)-2f(a)=0,
∴F(-x)=-F(x),∴函數F(x)=f(x+a)-f(a)為R上的奇函數,∴故②正確.
在③中,函數f(x)=x3-3x2+6x-2,
∴f(1+x)+f(1-x)=(1+x)3-3(1+x)2+6(1+x)-2+(1-x)3-3(1-x)2+6(1-x)-2=4,
∴點(1,2)為函數f(x)的“中心點”,故③正確.
故答案為:①②③.
點評 本題主要考查函數中心的定義的應用,綜合性較強,運算量量較大,難度較大.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
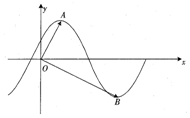 已知函數f(x)=Msin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分圖象如下圖所示,其中A,B分別為函數f(x)圖象的一個最高點和最低點,且A,B兩點的橫坐標分別為1,4,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,則函數f(x)的一個單調減區間為( )
已知函數f(x)=Msin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分圖象如下圖所示,其中A,B分別為函數f(x)圖象的一個最高點和最低點,且A,B兩點的橫坐標分別為1,4,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,則函數f(x)的一個單調減區間為( )| A. | (-6,-3) | B. | (6,9) | C. | (7,10) | D. | (10,13) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
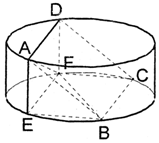 如圖,圓柱的高為2,底面半徑為3,AE,DF是圓柱的兩條母線,B、C是下底面圓周上的兩點,已知四邊形ABCD是正方形.
如圖,圓柱的高為2,底面半徑為3,AE,DF是圓柱的兩條母線,B、C是下底面圓周上的兩點,已知四邊形ABCD是正方形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com