
 (a>0,b>0)
(a>0,b>0)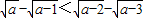 (a≥3)
(a≥3) <
<
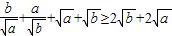 ,后移項即得;對于C,D:左右兩式平方后再進行比較大小即可.
,后移項即得;對于C,D:左右兩式平方后再進行比較大小即可. (a2+b2+c2+a2+b2+c2)
(a2+b2+c2+a2+b2+c2)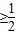 (2ab+2ca+2bc)=ab+bc+ca.
(2ab+2ca+2bc)=ab+bc+ca.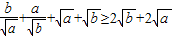 ,
,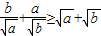 ,B成立.
,B成立.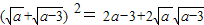 ,
,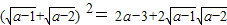 ,
,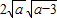
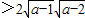 ,
,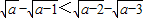 ,故C正確;
,故C正確;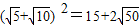 ,
,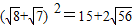 ,
,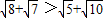 ,故D不正確.
,故D不正確.

湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com