
【題目】若函數f(x)=xlnx-a有兩個零點,則實數a的取值范圍為( )
A.[0,![]() )B.(0,
)B.(0,![]() )
)
C.(0,![]() ]D.(-
]D.(-![]() ,0)
,0)
【答案】D
【解析】
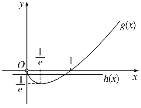
由函數f(x)=xlnx-a有兩個零點,利用![]() ,對參數與變量進行分離,轉化為
,對參數與變量進行分離,轉化為![]() ,令g(x)=xlnx,h(x)=a,則問題可轉化成函數g(x)與h(x)的圖像有兩個交點,利用求導的方法討論出
,令g(x)=xlnx,h(x)=a,則問題可轉化成函數g(x)與h(x)的圖像有兩個交點,利用求導的方法討論出![]() 的大致圖像,然后利用數形結合的方法即可求出a的取值范圍.
的大致圖像,然后利用數形結合的方法即可求出a的取值范圍.
令g(x)=xlnx,h(x)=a,則問題可轉化成函數g(x)與h(x)的圖像有兩個交點.g′(x)=lnx+1,令g′(x)<0,即lnx<-1,可解得0<x<![]() ;令g′(x)>0,即lnx>-1,可解得x>
;令g′(x)>0,即lnx>-1,可解得x>![]() ,所以,當0<x<
,所以,當0<x<![]() 時,函數g(x)單調遞減;當x>
時,函數g(x)單調遞減;當x>![]() 時,函數g(x)單調遞增,由此可知當x=
時,函數g(x)單調遞增,由此可知當x=![]() 時,g(x)min=-
時,g(x)min=-![]() .在同一坐標系中作出函數g(x)和h(x)的簡圖如圖所示,據圖可得-
.在同一坐標系中作出函數g(x)和h(x)的簡圖如圖所示,據圖可得-![]() <a<0.故選D.
<a<0.故選D.


科目:高中數學 來源: 題型:
【題目】某單位舉辦2010年上海世博會知識宣傳活動,進行現場抽獎,
盒中裝有9張大小相同的精美卡片,卡片上分別印有“世博會會徽” 或“海寶”(世博會吉祥物)圖案;抽獎規則是:參加者從盒中抽取卡片兩張,若抽到兩張都是“海寶”卡
即可獲獎,否則,均為不獲獎.卡片用后放回盒子,下一位參加者繼續重復進行.
(1)活動開始后,一位參加者問:盒中有幾張“海寶”卡?主持人答:我只知道,
從盒中抽取兩張都是“世博會會徽“卡的概率是![]() ,求抽獎者獲獎的概率;
,求抽獎者獲獎的概率;
(2)現有甲、乙、丙、丁四人依次抽獎,用![]() 表示獲獎的人數,求
表示獲獎的人數,求![]() 的分布列及
的分布列及![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數)的圖像與
為常數)的圖像與![]() 軸交于點
軸交于點![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() .
.
(1)求![]() 的值及函數
的值及函數![]() 的極值;
的極值;
(2)證明:當![]() 時,
時,![]() ;
;
(3)證明:對任意給定的正數![]() ,總存在
,總存在![]() ,使得當
,使得當![]() 時,恒有
時,恒有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求證:

(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的左右頂點,
的左右頂點,![]() 點為橢圓
點為橢圓![]() 上一點,點
上一點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,且
,且![]() .
.
(1)若橢圓![]() 經過圓
經過圓![]() 的圓心,求橢圓
的圓心,求橢圓![]() 的方程;
的方程;
(2)在(1)的條件下,若過點![]() 的直線與橢圓
的直線與橢圓![]() 相交于不同的
相交于不同的![]() 兩點,設
兩點,設![]() 為橢圓
為橢圓![]() 上一點,且滿足
上一點,且滿足![]() (
(![]() 為坐標原點),當
為坐標原點),當![]() 時,求實數
時,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC中,角A,B,C所對的邊分別為a,b,c,若(2b﹣c)cosA=acosC.
(1)求角A;
(2)若△ABC的外接圓面積為π,求△ABC的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司收取快遞費用的標準是:重量不超過![]() 的包裹收費
的包裹收費![]() 元;重量超過
元;重量超過![]() 的包裹,除
的包裹,除![]() 收費
收費![]() 元之外,超過
元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需再收
計算)需再收![]() 元.該公司將最近承攬的
元.該公司將最近承攬的![]() 件包裹的重量統計如下:
件包裹的重量統計如下:
包裹重量(單位: |
|
|
|
|
|
包裹件數 |
|
|
|
|
|
公司對近![]() 天,每天攬件數量統計如下表:
天,每天攬件數量統計如下表:
包裹件數范圍 |
|
|
|
|
|
包裹件數 (近似處理) |
|
|
|
|
|
天數 |
|
|
|
|
|
以上數據已做近似處理,并將頻率視為概率.
(1)計算該公司未來![]() 天內恰有
天內恰有![]() 天攬件數在
天攬件數在![]() 之間的概率;
之間的概率;
(2)(i)估計該公司對每件包裹收取的快遞費的平均值;
(ii)公司將快遞費的三分之一作為前臺工作人員的工資和公司利潤,剩余的用作其他費用.目前前臺有工作人員![]() 人,每人每天攬件不超過
人,每人每天攬件不超過![]() 件,工資
件,工資![]() 元.公司正在考慮是否將前臺工作人員裁減
元.公司正在考慮是否將前臺工作人員裁減![]() 人,試計算裁員前后公司每日利潤的數學期望,并判斷裁員是否對提高公司利潤更有利?
人,試計算裁員前后公司每日利潤的數學期望,并判斷裁員是否對提高公司利潤更有利?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型企業生產的某批產品細分為![]() 個等級,為了了解這批產品的等級分布情況,從倉庫存放的
個等級,為了了解這批產品的等級分布情況,從倉庫存放的![]() 件產品中隨機抽取
件產品中隨機抽取![]() 件進行檢測、分類和統計,并依據以下規則對產品進行打分:
件進行檢測、分類和統計,并依據以下規則對產品進行打分:![]() 級或
級或![]() 級產品打
級產品打![]() 分;
分;![]() 級或
級或![]() 級產品打
級產品打![]() 分;
分;![]() 級、
級、![]() 級、
級、![]() 級或
級或![]() 級產品打
級產品打![]() 分;其余產品打
分;其余產品打![]() 分.現在有如下檢測統計表:
分.現在有如下檢測統計表:
等級 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
頻數 | 10 | 90 | 100 | 200 | 200 | 100 | 100 | 100 | 70 | 30 |
規定:打分不低于![]() 分的為優良級.
分的為優良級.
(1)①試估計該企業庫存的![]() 件產品為優良級的概率;
件產品為優良級的概率;
②請估計該企業庫存的![]() 件產品的平均得分.
件產品的平均得分.
(2)從該企業庫存的![]() 件產品中隨機抽取
件產品中隨機抽取![]() 件,請估計這
件,請估計這![]() 件產品的打分之和為
件產品的打分之和為![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家之一,城市缺水問題較為突出.某市為了節約生活用水,計劃在本市試行居民生活用水定額管理(即確定一個居民月均用水量標準:用水量不超過a的部分按照平價收費,超過a的部分按照議價收費).為了較為合理地確定出這個標準,通過抽樣獲得了100位居民某年的月均用水量(單位:噸),制作了頻率分布直方圖,
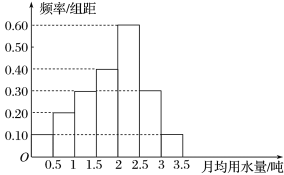
(Ⅰ)用該樣本估計總體:
(1)估計該市居民月均用水量的平均數;
(2)如果希望86%的居民每月的用水量不超出標準,則月均用水量a的最低標準定為多少噸?
(Ⅱ)若將頻率視為概率,現從該市某大型生活社區隨機調查3位居民的月均用水量,其中月均用水量不超過2.5噸的人數為X,求X的分布列和均值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com