【題目】某大型企業(yè)生產(chǎn)的某批產(chǎn)品細分為
個等級，為了了解這批產(chǎn)品的等級分布情況，從倉庫存放的
件產(chǎn)品中隨機抽取
件進行檢測、分類和統(tǒng)計，并依據(jù)以下規(guī)則對產(chǎn)品進行打分：
級或
級產(chǎn)品打
分；
級或
級產(chǎn)品打
分；
級、
級、
級或
級產(chǎn)品打
分；其余產(chǎn)品打
分.現(xiàn)在有如下檢測統(tǒng)計表：
等級 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
頻數(shù) | 10 | 90 | 100 | 200 | 200 | 100 | 100 | 100 | 70 | 30 |
規(guī)定：打分不低于分的為優(yōu)良級.
（1）①試估計該企業(yè)庫存的件產(chǎn)品為優(yōu)良級的概率；
②請估計該企業(yè)庫存的件產(chǎn)品的平均得分.
（2）從該企業(yè)庫存的件產(chǎn)品中隨機抽取件，請估計這件產(chǎn)品的打分之和為
分的概率.
【答案】（1）①
，②78；（2）
【解析】
（1）根據(jù)統(tǒng)計表，分別求出在
件產(chǎn)品中，分別求出打分為
分、
分、
分、
分對應(yīng)的概率，則優(yōu)良級的概率即為分、分對應(yīng)的概率之和；
（2）利用平均數(shù)公式
，即可估計出
件產(chǎn)品的平均得分；
（3）由題可知，
件產(chǎn)品的打分之和為
分，即為
或者
，再根據(jù)二項分布以及分類加法原則，求出概率.
解：在件產(chǎn)品中，設(shè)任意
件產(chǎn)品打分為分、分、分、分，
分別記為事件
，由統(tǒng)計表可得，
，
，
，
.
（1）①估計該企業(yè)庫存的件產(chǎn)品為優(yōu)良級的概率為
.
②估計該企業(yè)庫存的件產(chǎn)品的平均得分為
(分).
（2）因為
，
所以從該企業(yè)庫存的件產(chǎn)品隨機抽取件，估計這件產(chǎn)品的打分之和為分的概率為
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若函數(shù)f(x)＝xlnx－a有兩個零點，則實數(shù)a的取值范圍為( )
A.[0，
)B.(0，)
C.(0，]D.(－，0)
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，如圖，已知橢圓E：
的左、右頂點分別為
、
，上、下頂點分別為
、
．設(shè)直線
傾斜角的余弦值為
，圓
與以線段
為直徑的圓關(guān)于直線對稱．
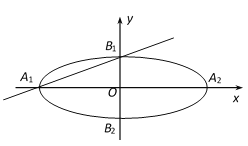
（1）求橢圓E的離心率；
（2）判斷直線與圓的位置關(guān)系，并說明理由；
（3）若圓的面積為
，求圓的方程．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
．
（1）設(shè)θ∈[0，π]，且f（θ）
1，求θ的值；
（2）在△ABC中，AB＝1，f（C）1，且△ABC的面積為
，求sinA+sinB的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）＝（x2+2x﹣3）ex；
（1）求f（x）在x＝0處的切線；
（2）求f（x）的單調(diào)區(qū)間.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】若數(shù)列{an}滿足a1＝1，a2＝1，an+2＝an+an+1，則稱數(shù)列{an}為斐波那契數(shù)列，斐波那契螺旋線是根據(jù)斐波那契數(shù)列畫出來的螺旋曲線，自然界中存在許多斐波那契螺旋線的圖案，是自然界最完美的經(jīng)典黃金比例.作圖規(guī)則是在以斐波那契數(shù)為邊的正方形拼成的長方形中畫一個圓心角為90°的扇形，連起來的弧線就是斐波那契螺旋線，如圖所示的7個正方形的邊長分別為a1，a2，…，a7，在長方形ABCD內(nèi)任取一點，則該點不在任何一個扇形內(nèi)的概率為（ ）
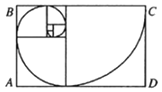
A.1
B.1
C.
D.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
