【題目】如圖，在直四棱柱ABCD－A1B1C1D1中，AD//平面BCC1B1，AD⊥DB.求證：
（1）BC//平面ADD1A1；
（2）平面BCC1B1⊥平面BDD1B1.
【答案】（1）證明見解析；（2）證明見解析.
【解析】
（1）由直線與平面平行的性質可得：由AD//平面BCC1B1，有AD//BC，同時AD平面ADD1A1，可得BC//平面ADD1A1；
（2）由（1）知AD//BC，因為AD⊥DB，所以BC⊥DB，同時由直四棱柱性質可得DD1⊥BC，BC⊥平面BDD1B1，可得證明.
解：（1）因為AD//平面BCC1B1，AD平面ABCD，平面BCC1B1∩平面ABCD=BC，
所以AD//BC.
又因為BC平面ADD1A1，AD平面ADD1A1，
所以BC//平面ADD1A1.
（2）由（1）知AD//BC，因為AD⊥DB，所以BC⊥DB，
在直四棱柱ABCD－A1B1C1D1中DD1⊥平面ABCD，BC底面ABCD，
所以DD1⊥BC，
又因為DD1平面BDD1B1，DB平面BDD1B1，DD1∩DB=D，
所以BC⊥平面BDD1B1，
因為BC平面BCC1B1，
所以平面BCC1B1⊥平面BDD1B1
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
平面
，底面是直角梯形，
，
，且
.點
是線段
上一點，且
.
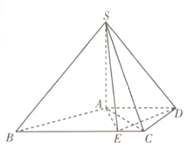
（1）求證：平面
平面
.
（2）若
，在線段
上是否存在一點
，使得到平面
的距離為
？若存在，求
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓O1與圓O：x2+y2＝r（r＞0）交于點P（﹣1，y0）.且關于直線x+y＝1對稱.
（1）求圓O及圓O1的方程：
（2）在第一象限內.圓O上是否存在點A，過點A作直線l與拋物線y2＝4x交于點B，與x軸交于點D，且以點D為圓心的圓過點O，A，B？若存在.求出點A的坐標；若不存在.說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
某投資公司在2010年年初準備將1000萬元投資到“低碳”項目上，現有兩個項目供選擇：
項目一：新能源汽車．據市場調研，投資到該項目上，到年底可能獲利
，也可能虧損
，且這兩種情況發生的概率分別為
和
；
項目二：通信設備．據市場調研，投資到該項目上，到年底可能獲利
，可能虧損，也可能不賠不賺，且這三種情況發生的概率分別為
、
和
（Ⅰ）針對以上兩個投資項目，請你為投資公司選擇一個合理的項目，并說明理由；
（Ⅱ）若市場預期不變，該投資公司按照你選擇的項目長期投資（每一年的利潤和本金繼續用作投資），問大約在哪一年的年底總資產（利潤＋本金）可以翻一番？
（參考數據：
，
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，如圖，已知橢圓E：
的左、右頂點分別為
、
，上、下頂點分別為
、
．設直線
傾斜角的余弦值為
，圓
與以線段
為直徑的圓關于直線對稱．
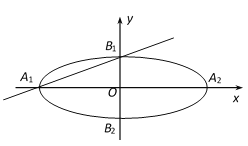
（1）求橢圓E的離心率；
（2）判斷直線與圓的位置關系，并說明理由；
（3）若圓的面積為
，求圓的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
