【題目】已知函數
在
處取得極值
．
（1）求函數
的解析式；
（2）設函數
，若對任意的
，總存在唯一的
（
為自然對數的底數）使得
，求實數
的取值范圍．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】某企業擬生產一種如圖所示的圓柱形易拉罐（上下底面及側面的厚度不計）.易拉罐的體積為
，設圓柱的高度為
，底面半徑為
，且
.假設該易拉罐的制造費用僅與其表面積有關.已知易拉罐側面制造費用為
元/ 
，易拉罐上下底面的制造費用均為
元/ 
（
， 
為常數，且
）.
（1）寫出易拉罐的制造費用
（元）關于
的函數表達式，并求其定義域；
（2）求易拉罐制造費用最低時
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝
x3＋
x2＋
x(0<a<1，x∈R)．若對于任意的三個實數x1，x2，x3∈[1,2]，都有f(x1)＋f(x2)>f(x3)恒成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝elnx，g(x)＝
f(x)－(x＋1)．(e＝2.718……)
(1)求函數g(x)的極大值；
(2)求證：1＋
＋
＋…＋
>ln(n＋1)(n∈N*)．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個盒子中裝有2個紅球，4個白球，除顏色外，它們的形狀、大小、質量等完全相同
（1）采用不放回抽樣，先后取兩次，每次隨機取一個球，求恰好取到1個紅球，七個白球的概率；
（2）采用放回抽樣，每次隨機抽取一球，連續取3次，求至少有1次取到紅球的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
），將
的圖象向左平移
個單位長度后得到
的圖象，且
在區間
內的最大值為
.
（1）求實數
的值；
（2）在
中，內角
， 
， 
的對邊分別是
， 
， 
，若
，且
，求
的周長
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種產品的廣告費支出
與銷售額
（單位：萬元）之間有如下對應數據：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求回歸直線方程；
（2）試預測廣告費支出為
萬元時，銷售額多大？
（3）在已有的五組數據中任意抽取兩組，求至少有一組數據其預測值與實際值之差的絕對值不超過
的概率.(參考數據：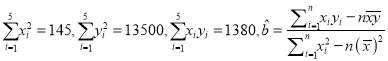 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一鮮花店一個月（30天）某種鮮花的日銷售量與銷售天數統計如下：
日銷售量（枝） | 0～49 | 50～99 | 100～149 | 150～199 | 200～250 |
銷售天數（天） | 3天 | 3天 | 15天 | 6天 | 3天 |
將日銷售量落入各組區間的頻率視為概率．
（1）試求這30天中日銷售量低于100枝的概率；
（2）若此花店在日銷售量低于100枝的6天中選擇2天作促銷活動，求這2天的日銷售量都低于50枝的概率（不需要枚舉基本事件）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
