Question

已知數列{a_n}的前n項和S_n=10n-n²（n∈N^*），又b_n=|a_n|（n∈N^*），求{b_n}的前n項和T_n．

Answer 1

解：由S_n=10n-n²可得S_n-1=10（n-1）-（n-1）²，（n≥2）
兩式相減可得a_n=11-2n
∵n=1時，a₁=S₁=10-1=9，滿足上式
∴a_n=11-2n，∴b_n=|11-2n|．
顯然n≤5時，b_n=a_n=11-2n，T_n=10n-n²．
n≥6時，b_n=-a_n=2n-11，
T_n=（a₁+a₂+…+a₅）-（a₆+a₇+…+a_n）=2S₅-S_n=50-10n+n²
故T_n=
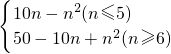
分析：由題意可得{b_n}是由一個首項為正值，而公差為負的一個等差數列，{a_n}的各項取絕對值后得到的一個新數列，因此求{b_n}的前n項和可轉化為求數列{a_n}的和的問題．
點評：本題考查數列的通項與求和，考查學生分析解決問題的能力，屬于中檔題．