解:(1)設P(x
0,y
0),Q(x
0,-y
0),
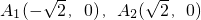
直線A
1P的方程為:
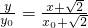
,(1)
直線A
2Q的方程為:
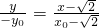
,(2)
將(1)×(2)得到:
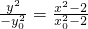
,又因為
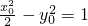
.
所以得到M的軌跡方程為:

,(y≠0)
(2)

,∴A,B,N三點共線,而點N的坐標為(-2,0).
設直線AB的方程為y=k(x+2),其中k為直線AB的斜率,依條件知k≠0.
由
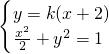
消去x得
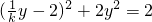
,即
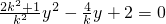
根據(jù)條件可知
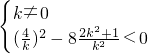
解得
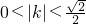
(5分)
設A(x
1,y
1),B(x
2,y
2),則根據(jù)韋達定理,得
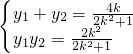
又由

得(x
1+2,y
1)=λ(x
2+2,y
2)
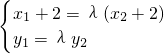
從而
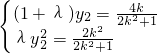
消去y
2得
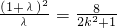
消去
令
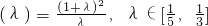
則
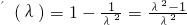
由于
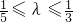
所以∅(λ)是區(qū)間
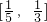
上的減函數(shù),
從而
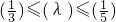
,即
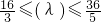
,
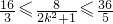
,∴
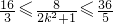
解得

而
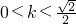
,∴
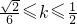
因此直線AB的斜率的取值范圍是
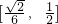
分析:(1)設P(x
0,y
0),Q(x
0,-y
0),從而可得直線A
1P的方程為:
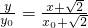
直線A
2Q的方程為:
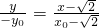
由兩式得到:
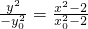
,結合
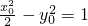
,可得M的軌跡方程
(2)

,∴A,B,N三點共線,及點N的坐標為(-2,0).可設直線AB的方程為y=k(x+2),其中k為直線AB的斜率,依條件知k≠0.,聯(lián)立方程
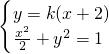
消去x得
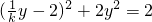
,即
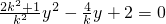
根據(jù)條件可知
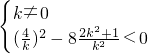
及
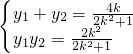
,又由

,建立坐標之間的關系,結合函數(shù)的單調性進行求解即可
點評:本題主要考查了由雙曲線的性質求解橢圓的方程,及直線與圓錐曲線的位置關系的綜合考查,要求考生具備一定的綜合能力及推理運算的能力,綜合性比較強.

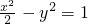 的左右兩個頂點,一條動弦垂直于x軸,且與雙曲線交于P,Q(P點位于x軸的上方),直線A1P與直線A2Q相交于點M,
的左右兩個頂點,一條動弦垂直于x軸,且與雙曲線交于P,Q(P點位于x軸的上方),直線A1P與直線A2Q相交于點M, ,其中
,其中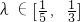 ,求出直線AB斜率的取值范圍.
,求出直線AB斜率的取值范圍.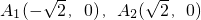
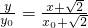 ,(1)
,(1)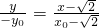 ,(2)
,(2)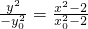 ,又因為
,又因為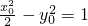 .
. ,(y≠0)
,(y≠0) ,∴A,B,N三點共線,而點N的坐標為(-2,0).
,∴A,B,N三點共線,而點N的坐標為(-2,0).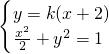 消去x得
消去x得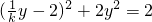 ,即
,即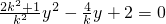
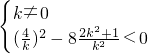 解得
解得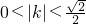 (5分)
(5分)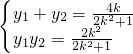
 得(x1+2,y1)=λ(x2+2,y2)
得(x1+2,y1)=λ(x2+2,y2)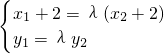 從而
從而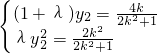 消去y2得
消去y2得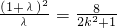 消去
消去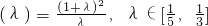 則
則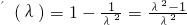
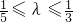 所以∅(λ)是區(qū)間
所以∅(λ)是區(qū)間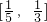 上的減函數(shù),
上的減函數(shù),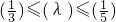 ,即
,即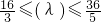 ,
,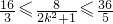 ,∴
,∴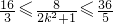 解得
解得
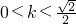 ,∴
,∴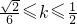
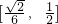
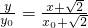 直線A2Q的方程為:
直線A2Q的方程為: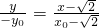 由兩式得到:
由兩式得到: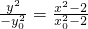 ,結合
,結合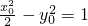 ,可得M的軌跡方程
,可得M的軌跡方程 ,∴A,B,N三點共線,及點N的坐標為(-2,0).可設直線AB的方程為y=k(x+2),其中k為直線AB的斜率,依條件知k≠0.,聯(lián)立方程
,∴A,B,N三點共線,及點N的坐標為(-2,0).可設直線AB的方程為y=k(x+2),其中k為直線AB的斜率,依條件知k≠0.,聯(lián)立方程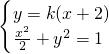 消去x得
消去x得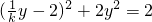 ,即
,即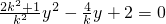
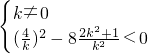 及
及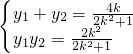 ,又由
,又由 ,建立坐標之間的關系,結合函數(shù)的單調性進行求解即可
,建立坐標之間的關系,結合函數(shù)的單調性進行求解即可

 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案 導學教程高中新課標系列答案
導學教程高中新課標系列答案 的左右兩個頂點,一條動弦垂直于x軸,且與雙曲線交于P,Q(P點位于x軸的上方),直線A1P與直線A2Q相交于點M,
的左右兩個頂點,一條動弦垂直于x軸,且與雙曲線交于P,Q(P點位于x軸的上方),直線A1P與直線A2Q相交于點M, ,其中
,其中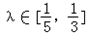 ,求出直線AB斜率的取值范圍.
,求出直線AB斜率的取值范圍.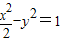 的左右兩個頂點,一條動弦垂直于x軸,且與雙曲線交于P,Q(P點位于x軸的上方),直線A1P與直線A2Q相交于點M,
的左右兩個頂點,一條動弦垂直于x軸,且與雙曲線交于P,Q(P點位于x軸的上方),直線A1P與直線A2Q相交于點M,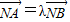 ,其中
,其中 ,求出直線AB斜率的取值范圍.
,求出直線AB斜率的取值范圍.