
 其中a>0,且a≠1,
其中a>0,且a≠1, 的定義域;
的定義域; ;
; 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.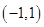 ;(2)
;(2)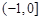 ;(3)m≤0。
;(3)m≤0。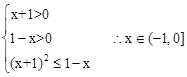 .
.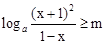 恒成立.
恒成立. 的取值范圍,再結合對數函數的單調性可求出
的取值范圍,再結合對數函數的單調性可求出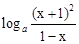 的最小值,讓m小于等于其最小值即可.
的最小值,讓m小于等于其最小值即可.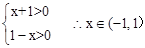 函數f(x)的定義域為
函數f(x)的定義域為 ………3分
………3分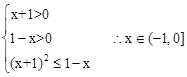 ……………………………………(8分)
……………………………………(8分)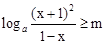 恒成立.……(9分)
恒成立.……(9分) ,令t=1-x,t∈(0,1],∴
,令t=1-x,t∈(0,1],∴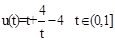 ……(10分)
……(10分)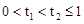
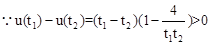
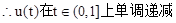 ,
,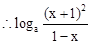 的最小值為0…………………(13分)
的最小值為0…………………(13分)

 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:高中數學 來源:不詳 題型:解答題
 的單調函數
的單調函數 是奇函數,當
是奇函數,當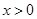 時,
時,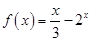 .
.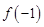 的值;
的值;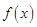 的解析式;
的解析式;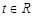 ,不等式
,不等式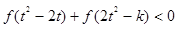 恒成立,求實數
恒成立,求實數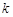 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
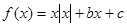 ,給出以下四個命題:①當c=0時,有
,給出以下四個命題:①當c=0時,有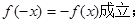 ②當b=0,c>0時,方程
②當b=0,c>0時,方程 ③函數
③函數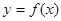 的圖象關于點(0,c)對稱 ④當x>0時;函數
的圖象關于點(0,c)對稱 ④當x>0時;函數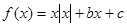 ,
, 。其中正確的命題的序號是_________。
。其中正確的命題的序號是_________。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com