
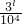 }={
}={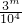 }={
}={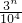 },其中{x}=x-[x],而[x]表示不超過x的最大整數.則這種三角形周長的最小值為________.
},其中{x}=x-[x],而[x]表示不超過x的最大整數.則這種三角形周長的最小值為________.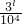 }={
}={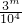 }={
}={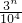 },可知3l、3m、3n的末四位數字相同即求滿足3l°3m≡3n( mod 104)的l、m、n,利用取余以及數的分析,即可求得結論.
},可知3l、3m、3n的末四位數字相同即求滿足3l°3m≡3n( mod 104)的l、m、n,利用取余以及數的分析,即可求得結論.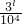 }={
}={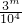 }={
}={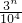 },∴3l、3m、3n的末四位數字相同,,
},∴3l、3m、3n的末四位數字相同,,

 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:高中數學 來源: 題型:
| 3l |
| 104 |
| 3m |
| 104 |
| 3n |
| 104 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
| 3l |
| 104 |
| 3m |
| 104 |
| 3n |
| 104 |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省珠海一中高三(下)第一次調研數學試卷(理科)(解析版) 題型:填空題
 }={
}={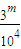 }={
}={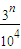 },其中{x}=x-[x],而[x]表示不超過x的最大整數.則這種三角形周長的最小值為 .
},其中{x}=x-[x],而[x]表示不超過x的最大整數.則這種三角形周長的最小值為 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com