【題目】某校舉行環保知識大獎賽，比賽分初賽和決賽兩部分，初賽采用選手選一題答一題的方式進行，每位選手最多有5次選題答題的機會，選手累積答對3題或打錯3題即終止其初賽的比賽：答對3題者直接進入初賽，打錯3題者則被淘汰.已知選手甲答對每個問題的概率相同，并且相互之間沒有影響，答題連續兩次答錯的概率為
.
（1）求選手甲可進入決賽的概率.
（2）設選手甲在初賽中答題的個數為
，試求
的分布列，并求
的數學期望.
【答案】（1）P
（2）見解析
【解析】試題分析： 
設選手甲任答一題，正確的概率為
，根據甲答對每個問題的概率相同，并且相互之間沒有影響，答題連續兩次打錯的概率為
，列出關于
的方程，得到甲答對題目的概率，選手甲能夠進入決賽包括兩種情況，這兩種情況是互斥的，由互斥事件的概率公式計算得到答案；
的取值為
， 
， 
，對應的事件分別是前三個題全部答對，前四個題答對了三個，其中第四題一定對，前五個題答對了三個，第五個一定答對，分別求出它們的概率，列出分布列，求出期望；
解析：（1）設選手甲任答一題，正確的概率為
，依題意
， 
，
選手甲可進入決賽的概率
.
（2）隨機變量
所有可能取值為
， 
， 
，
依題意
，
，
，
故隨機變量
的分布列為：
|
|
|
|
|
|
|
|
.
科目：高中數學 來源： 題型：
【題目】有下列命題：（1）終邊相同的角的同名三角比的值相等；（2）終邊不同的角的同名三角比的值不同；（3）若
，則
是第一或第二象限角；（4）△
中，若
，則
；其中正確命題的個數是（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
過點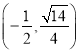
，且離心率為
.過點
的直線
與橢圓
交于
， 
兩點.
（Ⅰ）求橢圓
的標準方程；
（Ⅱ）若點
為橢圓
的右頂點，探究： 
是否為定值，若是，求出該定值，若不是，請說明理由.（其中， 
， 
分別是直線
、
的斜率）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在高中學習過程中，同學們常這樣說：“如果你的物理成績好，那么你的數學學習就不會有什么大問題．”某班針對“高中物理學習對數學學習的影響”進行研究，得到了學生的物理成績與數學成績具有線性相關關系，如表為該班隨機抽取6名學生在一次考試中的物理和數學成績：
學生編號 學科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成績（x） | 75 | 65 | 75 | 65 | 60 | 80 |
數學成績（y） | 125 | 117 | 110 | 103 | 95 | 110 |
（1）求數學成績y對物理成績x的線性回歸方程；
（2）該班某同學的物理成績100分，預測他的數學成績．
參考公式：回歸方程
中斜率和截距的最小二乘估計公式分別為：
，
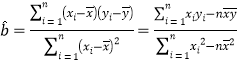參考數據：752+652+752+652+602+802＝29700，
75×125+65×117+75×110+65×103+60×95+80×110＝46425．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
，其圖象在點
處切線的斜率為-3.
（1）求
與
關系式；
（2）求函數
的單調區間（用只含有
的式子表示）；
（3）當
時，令
，設
是函數
的兩個零點， 
是
與
的等差中項，求證： 
（
為函數
的導函數）.
查看答案和解析>>
科目：高中數學 來源： 題型：
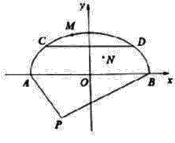
【題目】某經濟開發區規劃要修建一地下停車場，停車場橫截面是如圖所示半橢圓形AMB，其中AP為2百米，BP為4百米，
，M為半橢圓上異于A，B的一動點，且
面積最大值為
平方百米，如圖建系．
求出半橢圓弧的方程；
若要將修建地下停車場挖出的土運到指定位置P處，N為運土點，以A,B為出口，要使運土最省工，工程部需要指定一條分界線，請求出分界線所在的曲線方程；
若在半橢圓形停車場的上方修建矩形商場，矩形的一邊CD與AB平行，設
百米，試確定t的值，使商場地面的面積最大．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）＝（e－x－ex）
，則不等式f（x）＜f（1＋x）的解集為（ ）
A. （0，＋∞） B. （－∞，－
）
C. （－，＋∞） D. （－，0）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
