
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
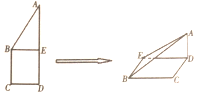 如圖所示,正方形BCDE的邊長為a,已知$AB=\sqrt{3}BC$,將△ABE沿BE邊折起,折起后A點在平面BCDE上的射影為D點,則翻折后的幾何體中有如下描述:
如圖所示,正方形BCDE的邊長為a,已知$AB=\sqrt{3}BC$,將△ABE沿BE邊折起,折起后A點在平面BCDE上的射影為D點,則翻折后的幾何體中有如下描述:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{25}{4}$ | B. | $\frac{31}{4}$ | C. | $\frac{37-6\sqrt{3}}{4}$ | D. | $\frac{37-2\sqrt{33}}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com