
【題目】為了解今年某校高三畢業班準備報考飛行員學生的體重情況,將所得的數據整理后,畫出了頻率分布直方圖(如圖),已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數為15.
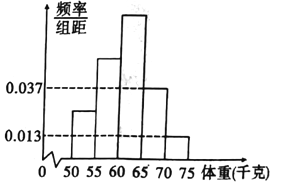
(1)求該校報考飛行員的總人數;
(2)以這所學校的樣本數據來估計全省的總體數據,若從全省報考飛行員的同學中(人數很多)任選三人,設![]() 表示體重超過65公斤的學生人數,求
表示體重超過65公斤的學生人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
【答案】(1)60人;(2)詳見解析.
【解析】試題分析:根據前3組的頻率之比設出前3組的頻率,根據頻率分布直方圖中的數據計算后兩組的頻率,根據頻率和為1,計算出各組的頻率,利用第2 組的頻數為15,計算總人數; ![]() 表示體重超過65公斤的學生人數,利用直方圖求出體重超過65公斤的學生的頻率,寫出X的可取值,符合二項分布,根據二項分布數學期望公式求出數學期望.
表示體重超過65公斤的學生人數,利用直方圖求出體重超過65公斤的學生的頻率,寫出X的可取值,符合二項分布,根據二項分布數學期望公式求出數學期望.
試題解析:
(Ⅰ)設圖中從左到右的前3個小組的頻率分別為![]()
則![]() 解得
解得![]() ,
,
∵第2小組的頻數為15,頻率為![]() ,
,
∴該校報考飛行員的總人數為: ![]() (人).
(人).
(Ⅱ)體重超過65公斤的學生的頻率為![]()
∴X的可能取值為0,1,2,3,且![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
∴![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
由于![]() ,
, ![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】設△ABC的三內角A、B、C的對邊分別是a、b、c,且b(sinB﹣sinC)+(c﹣a)(sinA+sinC)=0 (Ⅰ)求角A的大小;
(Ⅱ)若a= ![]() ,sinC=
,sinC= ![]() sinB,求△ABC的面積.
sinB,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著資本市場的強勢進入,互聯網共享單車“忽如一夜春風來”,遍布了一二線城市的大街小巷.為了解共享單車在![]() 市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中抽取了200人進行抽樣分析,得到表格:(單位:人)
市的使用情況,某調查機構借助網絡進行了問卷調查,并從參與調查的網友中抽取了200人進行抽樣分析,得到表格:(單位:人)
經常使用 | 偶爾或不用 | 合計 | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
(1)根據以上數據,能否在犯錯誤的概率不超過0.15的前提下認為![]() 市使用共享單車情況與年齡有關?
市使用共享單車情況與年齡有關?
(2)現從所抽取的30歲以上的網友中利用分層抽樣的方法再抽取5人.
(i)分別求這5人中經常使用、偶爾或不用共享單車的人數;
(ii)從這5人中,再隨機選出2人贈送一件禮品,求選出的2人中至少有1人經常使用共享單車的概率.
參考公式:  ,其中
,其中![]() .
.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,滿足x2+y2≤1,x≥0,y≥0的點P(x,y)的集合對應的平面圖形的面積為 ![]() ;類似的,在空間直角坐標系O﹣xyz中,滿足x2+y2+z2≤1,x≥0,y≥0,z≥0的點P(x,y,z)的集合對應的空間幾何體的體積為( )
;類似的,在空間直角坐標系O﹣xyz中,滿足x2+y2+z2≤1,x≥0,y≥0,z≥0的點P(x,y,z)的集合對應的空間幾何體的體積為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 是奇函數,f(x)=lg(10x+1)+bx是偶函數.
是奇函數,f(x)=lg(10x+1)+bx是偶函數.
(1)求a和b的值.
(2)說明函數g(x)的單調性;若對任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求實數k的取值范圍.
(3)設 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求實數a的取值范圍.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB切⊙O于點B,直線AO交⊙O于D,E兩點,BC⊥DE,垂足為C.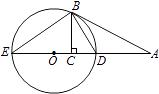
(1)證明:∠CBD=∠DBA;
(2)若AD=3DC,BC= ![]() ,求⊙O的直徑.
,求⊙O的直徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com