【答案】
分析:先令f(x)=
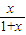
(x≥0),證f(x)單調遞增,再利用其單調性對不等式左式進行兩次放縮即可.
解答:證明:令f(x)=
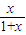
(x≥0),易證f(x)在[0,+∞)上單調遞增.
|a+b|≤|a|+|b|,
∴f(|a+b|)≤f(|a|+|b|),
即
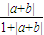
≤
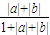
=
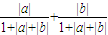
≤
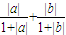
.
點評:在證明不等式的時候,在直接證明遇到困難的時候,可以利用不等式的傳遞性,把要證明的不等式加強為一個易證的不等式,即欲證A>B,我們可以適當的找一個中間量C作為媒介,證明A>C且C>B,從而得到A>B.我們把這種把B放大到C(或把A縮小到C)的方法稱為放縮法.

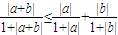 .
.