
已知函數
(1)求 的值域;
的值域;
(2)設 ,函數
,函數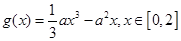 .若對任意
.若對任意 ,總存在
,總存在 ,使
,使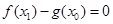 ,求實數
,求實數 的取值范圍.
的取值范圍.
(1) 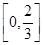 ;(2)
;(2)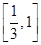
解析試題分析:(1)求出 的導函數,令導函數等于求出
的導函數,令導函數等于求出 的值,然后由
的值,然后由 的值,分區間討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值即可得到
的值,分區間討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值即可得到 的值域;(2)設函數
的值域;(2)設函數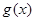 在[0,2]上的值域是A,根據題意對任意
在[0,2]上的值域是A,根據題意對任意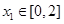 ,總存在
,總存在 ,使
,使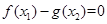 ,得到區間
,得到區間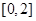 是A的子集,求出
是A的子集,求出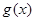 的導函數,分
的導函數,分 小于0和
小于0和 大于0兩種情況討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值,即可得到函數在相應區間的值域,根據區間[0,2]是A的子集判斷出符合這一條件的情況,列出關于
大于0兩種情況討論導函數的正負得到函數的單調區間,根據函數的增減性得到函數的最大值和最小值,即可得到函數在相應區間的值域,根據區間[0,2]是A的子集判斷出符合這一條件的情況,列出關于 的不等式,求出不等式的解集即可得到滿足題意
的不等式,求出不等式的解集即可得到滿足題意 的取值范圍.
的取值范圍.
試題解析:(1)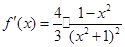 ,令
,令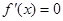 ,得
,得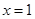 或
或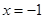 .
.
當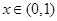 時,
時,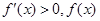 在
在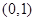 上單調遞增;
上單調遞增;
當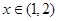 時,
時,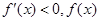 在
在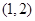 上單調遞減,
上單調遞減,
而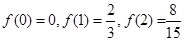 ,
,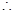 當
當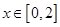 時,
時, 的值域是
的值域是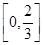 .
.
(2)設函數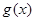 在
在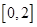 上的值域是A,
上的值域是A,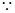 若對任意
若對任意 .總存在
.總存在 1,使
1,使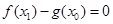 ,
,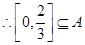 .
. 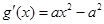 .
.
①當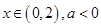 時,
時,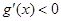 ,
,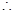 函數
函數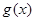 在
在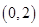 上單調遞減.
上單調遞減. 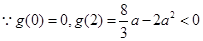 ,當
,當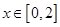 時,不滿足
時,不滿足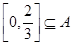 ;
;
②當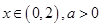 時,
時,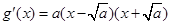 ,令
,令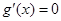 ,得
,得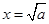 或
或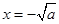 (舍去)
(舍去)
(i)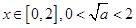 時,
時,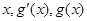 的變化如下表:
的變化如下表: