【題目】已知橢圓
的左、右焦點分別為F1(－c，0)，F2(c，0)，直線
交橢圓E于A，B兩點，△ABF1的周長為16，△AF1F2的周長為12．
(1)求橢圓E的標準方程與離心率；
(2)若直線l與橢圓E交于C，D兩點，且P(2，2)是線段CD的中點，求直線l的一般方程．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】在直角坐標系中，以原點為極點，x軸的正半軸為極軸建立極坐標系，已知曲線C： 
，過點
的直線l的參數方程為：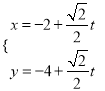 
(t為參數)，直線l與曲線C分別交于M、N兩點．
(Ⅰ)寫出曲線C的直角坐標方程和直線l的普通方程；
(Ⅱ)若| PM |，| MN |，| PN |成等比數列，求a的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“雙十一”期間，某淘寶店主對其商品的上架時間
（分鐘）和銷售量
（件）的關系作了統計，得到如下數據：
經計算： 
， 
， 
， 
.
（1）該店主通過作散點圖，發現上架時間與銷售量線性相關，請你幫助店主求出上架時間與銷售量的線性回歸方程（保留三位小數），并預測商品上架1000分鐘時的銷售量；
（2）從這11組數據
中任選2組，設
且
的數據組數為
，求
的分布列與數學期望.
附：線性回歸方程公式：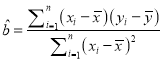 
， 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f(x)＝ln x，g(x)＝
x|x|.
(1)求g(x)在x＝－1處的切線方程；
(2)令F(x)＝x·f(x)－g(x)，求F(x)的單調區間；
(3)若任意x1，x2∈[1，＋∞)且x1>x2，都有m[g(x1)－g(x2)]>x1f(x1)－x2f(x2)恒成立，求實數m的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
的定義域為
，如果
， 
，使
（
為常數）成立，則稱函數
在
上的均值為
．給出下列四個函數：①
；②
；③
；④
．則其中滿足在其定義域上均值為2的函數是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“雙十一”期間，某淘寶店主對其商品的上架時間
（分鐘）和銷售量
（件）的關系作了統計，得到如下數據：
經計算： 
， 
， 
， 
.
（1）從滿足
的數據
中任取兩個，求所得兩個數據都滿足
的概率；
（2）該店主通過作散點圖，發現上架時間與銷售量線性相關，請你幫助店主求出上架時間與銷售量的線性回歸方程（保留三位小數），并預測商品上架1000分鐘時的銷售量.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】網上購物逐步走進大學生活,某大學學生宿舍4人積極參加網購,大家約定:每個人通過擲一枚質地均勻的骰子決定自己去哪家購物,擲出點數為5或6的人去淘寶網購物,擲出點數小于5的人去京東商城購物,且參加者必須從淘寶網和京東商城選擇一家購物.
(1)求這4個人中恰有2人去淘寶網購物的概率;
(2)求這4個人中去淘寶網購物的人數大于去京東商城購物的人數的概率:
(3)用X,Y分別表示這4個人中去淘寶網購物的人數和去京東商城購物的人數,記
,求隨機變量
的分布列與數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a，b，c分別是△ABC內角A，B，C的對邊，函數f(x)＝3＋2
sin xcos x＋2cos2x且f(A)＝5.
(1)求角A的大小；
(2)若a＝2，求△ABC面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
