
| A. | c<a<b | B. | b<c<a | C. | a<c<b | D. | c<b<a |
分析 根據條件xf′(x)-f(x)>0恒成立,構造函數g(x)=$\frac{f(x)}{x}$,然后根據導數和函數單調性之間的關系即可得到結論.
解答 解:構造函數g(x)=$\frac{f(x)}{x}$,
則g'(x)=$\frac{1}{{x}^{2}}$[f(x)-xf′(x)],
∵當x∈(0,+∞)時,xf′(x)-f(x)>0恒成立,
∴g'(x)<0,
即g(x)在(0,+∞)單調遞減,
∵a=f(1)=$\frac{f(1)}{1}$=g(1),b=$\frac{1}{2}$f(2)=$\frac{f(2)}{2}$=g(2),c=$\frac{\sqrt{2}}{2}$f($\sqrt{2}$)=$\frac{f(\sqrt{2})}{\sqrt{2}}$=g($\sqrt{2}$)
又1<$\sqrt{2}$<2,
∴g(1)>g($\sqrt{2}$)>g(2),
即a>c>b,
故選:B.
點評 本題主要考查函數值的大小比較,根據條件構造函數g(x)=$\frac{f(x)}{x}$是解決本題的關鍵,要求熟練掌握函數的單調性和導數之間的關系.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
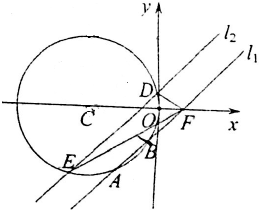 已知直線l1:y=x-1與圓C:(x+a)2+y2=a2(a>0)相交于A、B兩點,|AB|=2,直線l2∥l1,直線l2與圓C相交于D、E兩點.
已知直線l1:y=x-1與圓C:(x+a)2+y2=a2(a>0)相交于A、B兩點,|AB|=2,直線l2∥l1,直線l2與圓C相交于D、E兩點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com