
【題目】已知點A(t,1)為函數(shù)y=ax2+bx+4(a,b為常數(shù),且a≠0)與y=x圖象的交點.
(1)求t;
(2)若函數(shù)y=ax2+bx+4的圖象與x軸只有一個交點,求a,b;
(3)若1≤a≤2,設(shè)當(dāng)![]() ≤x≤2時,函數(shù)y=ax2+bx+4的最大值為m,最小值為n,求m﹣n的最小值.
≤x≤2時,函數(shù)y=ax2+bx+4的最大值為m,最小值為n,求m﹣n的最小值.
【答案】(1)t=1;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)把A(t,1)代入y=x即可得到結(jié)論;
(2)根據(jù)題意得方程組,解方程組即可得到結(jié)論;
(3)把A(1,1)代入y=ax2+bx+4得,b=3a,繼而得到對稱軸為直線x=![]() ,根據(jù)1≤a≤2,得到對稱軸的取值范圍
,根據(jù)1≤a≤2,得到對稱軸的取值范圍![]() ≤x≤2,當(dāng)x=
≤x≤2,當(dāng)x=![]() 時,得到m=
時,得到m=![]() ,當(dāng)x=2時,得到n=
,當(dāng)x=2時,得到n=![]() ,即可得到結(jié)論.
,即可得到結(jié)論.
解:(1)把A(t,1)代入y=x得t=1;
(2)∵y=ax2+bx+4的圖象與x軸只有一個交點,
∴![]() ,
,
∴![]() 或
或![]() ;
;
(3)把A(1,1)代入y=ax2+bx+4得,b=﹣3﹣a,
∴y=ax2﹣(a+3)x+4=a(x﹣![]() )2﹣
)2﹣![]() ,
,
∴對稱軸為直線x=![]() ,
,
∵1≤a≤2,
∴![]() ≤x=
≤x=![]() ≤2,
≤2,
∵![]() ≤x≤2,
≤x≤2,
∴當(dāng)x=![]() 時,y=ax2+bx+4的最大值為m=
時,y=ax2+bx+4的最大值為m=![]() ,
,
當(dāng)x=2時,n=﹣![]() ,
,
∴m﹣n=![]() ,
,
∵1≤a≤2,
∴當(dāng)a=2時,m﹣n的值最小,
即m﹣n的最小值![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
小學(xué)期末標(biāo)準(zhǔn)試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某射擊運動員,每次擊中目標(biāo)的概率都是![]() .現(xiàn)采用隨機模擬的方法估計該運動員射擊
.現(xiàn)采用隨機模擬的方法估計該運動員射擊![]() 次至少擊中
次至少擊中![]() 次的概率:先由計算器算出
次的概率:先由計算器算出![]() 到
到![]() 之間取整數(shù)值的隨機數(shù),指定
之間取整數(shù)值的隨機數(shù),指定![]() ,
,![]() 表示沒有擊中目標(biāo),
表示沒有擊中目標(biāo),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示擊中目標(biāo);因為射擊
表示擊中目標(biāo);因為射擊![]() 次,故以每
次,故以每![]() 個隨機數(shù)為一組,代表射擊
個隨機數(shù)為一組,代表射擊![]() 次的結(jié)果.經(jīng)隨機模擬產(chǎn)生了如下
次的結(jié)果.經(jīng)隨機模擬產(chǎn)生了如下![]() 組隨機數(shù):
組隨機數(shù):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
據(jù)此估計,該射擊運動員射擊![]() 次至少擊中
次至少擊中![]() 次的概率為( )
次的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某單位共有500名職工,其中不到35歲的有125人,35-49歲的有a人,50歲及以上的有b人,現(xiàn)用分層抽樣的方法,從中抽出100名職工了解他們的健康情況:
(1)求不到35歲的職工要抽取的人數(shù);
(2)如果已知35-49歲的職工抽取了56人,求a的值,并求50歲及以上的職工要抽取的人數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數(shù)![]() (
(![]() ),若
),若![]() 的解集是
的解集是![]() .
.
(1)求![]() 的值;
的值;
(2)若關(guān)于![]() 的不等式
的不等式![]() 有解,求實數(shù)
有解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
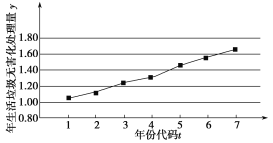
【題目】如圖是我國2012年至2018年生活垃圾無害化處理量(單位:億噸)的折線圖.注:年份代碼1~7分別對應(yīng)年份2012~2018.
(1)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系,請用相關(guān)系數(shù)加以說明;
的關(guān)系,請用相關(guān)系數(shù)加以說明;
(2)建立![]() 關(guān)于
關(guān)于![]() 的回歸方程(系數(shù)精確到0.01),預(yù)測2020年我國生活垃圾無害化處理量.
的回歸方程(系數(shù)精確到0.01),預(yù)測2020年我國生活垃圾無害化處理量.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關(guān)系數(shù)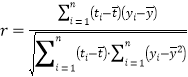 ,回歸方程
,回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為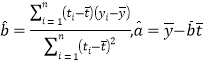 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司為了適應(yīng)市場需求對產(chǎn)品結(jié)構(gòu)做了重大調(diào)整,調(diào)整后初期利潤增長迅速,之后增長越來越慢,若要建立恰當(dāng)?shù)暮瘮?shù)模型來反映該公司調(diào)整后利潤![]() 與時間
與時間![]() 的關(guān)系,可選用
的關(guān)系,可選用
A.一次函數(shù)B.二次函數(shù)
C.指數(shù)型函數(shù)D.對數(shù)型函數(shù)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(1)若對于任意的![]() ,
, ![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,設(shè)函數(shù)
,設(shè)函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值、最小值分別為
上的最大值、最小值分別為![]() 、
、![]() ,記
,記![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知過點![]() 的橢圓
的橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() 、
、![]() ,
, ![]() 為橢圓上的任意一點,且
為橢圓上的任意一點,且![]() ,
, ![]() ,
, ![]() 成等差數(shù)列.
成等差數(shù)列.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)直線![]() :
: ![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩點,若點
兩點,若點![]() 始終在以
始終在以![]() 為直徑的圓外,求實數(shù)
為直徑的圓外,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com