
某小區想利用一矩形空地 建市民健身廣場,設計時決定保留空地邊上的一水塘(如圖中陰影部分),水塘可近似看作一個等腰直角三角形,其中
建市民健身廣場,設計時決定保留空地邊上的一水塘(如圖中陰影部分),水塘可近似看作一個等腰直角三角形,其中 ,
,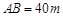 ,且
,且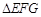 中,
中,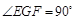 ,經測量得到
,經測量得到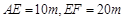 .為保證安全同時考慮美觀,健身廣場周圍準備加設一個保護欄.設計時經過點
.為保證安全同時考慮美觀,健身廣場周圍準備加設一個保護欄.設計時經過點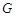 作一直線交
作一直線交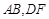 于
于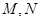 ,從而得到五邊形
,從而得到五邊形 的市民健身廣場,設
的市民健身廣場,設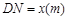 .
.
(1)將五邊形 的面積
的面積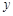 表示為
表示為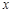 的函數;
的函數;
(2)當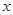 為何值時,市民健身廣場的面積最大?并求出最大面積.
為何值時,市民健身廣場的面積最大?并求出最大面積.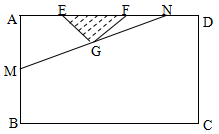
(1)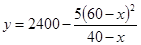 ;(2)當
;(2)當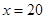 時,到的市民健身廣場面積最大,最大面積為
時,到的市民健身廣場面積最大,最大面積為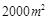 .
.
解析試題分析:(1)根據題意分析可考慮作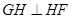 ,垂足為
,垂足為 ,從而可將五邊形的面積轉化為梯形
,從而可將五邊形的面積轉化為梯形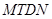 與矩形
與矩形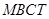 的面積之和,由
的面積之和,由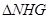 ∽
∽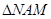 結合條件,可將梯形
結合條件,可將梯形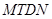 的上底,下底與高以及矩形
的上底,下底與高以及矩形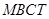 的長和寬都用含
的長和寬都用含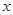 的代數式表示出來,從而可得:
的代數式表示出來,從而可得: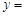
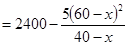 ,再由
,再由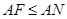 ,可得
,可得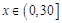 ;(2)由(1)及條件可知,問題就等價于求函數
;(2)由(1)及條件可知,問題就等價于求函數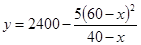 在
在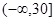 上的最大值,而將其變形后可得:
上的最大值,而將其變形后可得: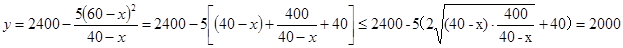 ,
,
當且僅當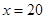 時,“=”成立,從而當
時,“=”成立,從而當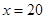 時,到的市民健身廣場面積最大,最大面積為
時,到的市民健身廣場面積最大,最大面積為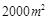 .
.
試題解析:(1)如圖,作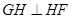 ,垂足為
,垂足為 ,
,
∵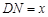 ,∴
,∴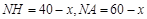 ,又由
,又由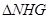 ∽
∽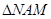 ,∴
,∴ ,
,
∵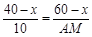 ,∴
,∴ , 2分
, 2分
過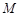 作
作 交
交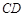 于
于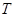 ,
,
則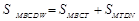
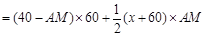 ,
,
所以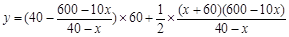
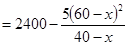 , 7分
, 7分
由于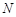 與
與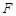 重合時,
重合時,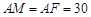 適合條件,故
適合條件,故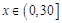 ; 8分
; 8分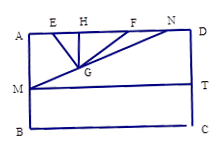
(2)由(1)得: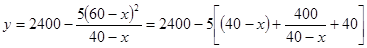 , 10分
, 10分
∴當且僅當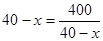 ,即
,即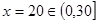 時,
時, 取得最大值
取得最大值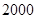 , 13分
, 13分
即當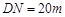 時,得到的市民健身廣場面積最大,最大面積為
時,得到的市民健身廣場面積最大,最大面積為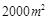 . 14分
. 14分
考點:1.函數的運用;2.基本不等式求最值.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)對任意實數x,y恒有f(x+y)=f(x)+f(y),且當x>0時,f(x)<0,又f(1)=-2.
(1)判斷f(x)的奇偶性;
(2)求證:f(x)是R上的減函數;
(3)求f(x)在區間[-3,3]上的值域;
(4)若?x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,把邊長為10的正六邊形紙板剪去相同的六個角,做成一個底面為正六邊形的無蓋六棱柱盒子,設其高為h,體積為V(不計接縫).
(1)求出體積V與高h的函數關系式并指出其定義域;
(2)問當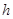 為多少時,體積V最大?最大值是多少?
為多少時,體積V最大?最大值是多少?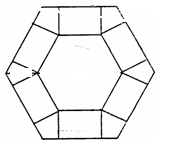
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com