【題目】若函數(shù)
在區(qū)間
上存在零點，則實數(shù)
的取值范圍為( )
A. 
B. 
C. 
D. 
【答案】D
【解析】
利用導(dǎo)數(shù)研究函數(shù)
在
上的單調(diào)性，當(dāng)
時，在上為增函數(shù)，
且
，即可判斷其沒有零點，不符合條件；當(dāng)
時，在上先減后增，有最小值且小于零，再結(jié)合冪函數(shù)和對數(shù)函數(shù)的增長速度大小關(guān)系，即可判斷當(dāng)
趨于
時，趨于，由零點存在性定理即可判斷其必有零點，符合題意，從而確定
的范圍.
因為函數(shù)
，
所以
令
，因為
，
當(dāng)
時，
，所以
所以
在上為增函數(shù)，則
，
當(dāng)
時，
，所以
，所以在上為增函數(shù)，
則，所以在上沒有零點.
當(dāng)
時，即，因為在上為增函數(shù)，則存在唯一的
，使得
，且當(dāng)
時，
，當(dāng)
時，；
所以當(dāng)時，
，為減函數(shù)，當(dāng)時，，為增函數(shù)，當(dāng)
時，
，
因為
，當(dāng)趨于時，趨于，
所以在內(nèi)，一定存在一個零點.
所以
，
故答案選D.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在水平地面上的不同兩點處栽有兩根筆直的電線桿，假設(shè)它們都垂直于地面，則在水平地面上視它們上端仰角相等的點
的軌跡可能是（ ）
①直線 ②圓 ③橢圓 ④拋物線
A.①②B.①③C.①②③D.②④
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，直線
的參數(shù)方程為
（
為參數(shù)）.以原點
為極點，以
軸為非負半軸為極軸建立極坐標(biāo)系，兩坐標(biāo)系相同的長度單位.圓
的方程為
被圓截得的弦長為
.
（Ⅰ）求實數(shù)
的值；
（Ⅱ）設(shè)圓與直線交于點
，若點
的坐標(biāo)為
，且
，求
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某網(wǎng)站舉行“衛(wèi)生防疫”的知識競賽網(wǎng)上答題，共有120000人通過該網(wǎng)站參加了這次競賽，為了解競賽成績情況，從中抽取了100人的成績進行統(tǒng)計，其中成績分組區(qū)間為
，
，
，
，
，其頻率分布直方圖如圖所示，請你解答下列問題：
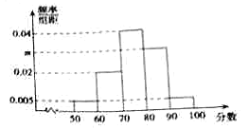
（1）求
的值；
（2）成績不低于90分的人就能獲得積分獎勵，求所有參賽者中獲得獎勵的人數(shù)；
（3）根據(jù)頻率分布直方圖，估計這次知識競賽成績的平均分（用組中值代替各組數(shù)據(jù)的平均值）.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知線段
是過拋物線
的焦點F的一條弦，過點A（A在第一象限內(nèi)）作直線
垂直于拋物線的準(zhǔn)線，垂足為C，直線
與拋物線相切于點A，交x軸于點T，給出下列命題：
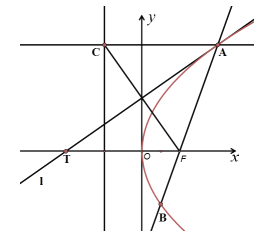
（1）
；
（2）
；
（3）
.
其中正確的命題個數(shù)為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】甲、乙兩人在相同條件下各射擊
次，每次中靶環(huán)數(shù)情況如圖所示：
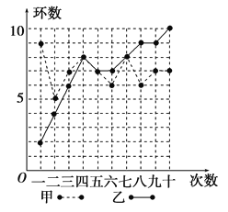
（1）請?zhí)顚懴卤恚ㄏ葘懗鲇嬎氵^程再填表）：
平均數(shù) | 方差 | 命中 | |
甲 |
|
|
|
乙 |
（2）從下列三個不同的角度對這次測試結(jié)果進行
①從平均數(shù)和方差相結(jié)合看（分析誰的成績更穩(wěn)定）；
②從平均數(shù)和命中
環(huán)及環(huán)以上的次數(shù)相結(jié)合看（分析誰的成績好些）；
③從折線圖上兩人射擊命中環(huán)數(shù)的走勢看（分析誰更有潛力）.
參考公式：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】給出下列五個命題：
①已知直線
、
和平面
，若
，
，則
；
②平面上到一個定點和一條定直線的距離相等的點的軌跡是一條拋物線；
③雙曲線
，則直線
與雙曲線有且只有一個公共點；
④若兩個平面垂直，那么一個平面內(nèi)與它們的交線不垂直的直線與另一個平面也不垂直；
⑤過
的直線
與橢圓
交于
、
兩點，線段
中點為
，設(shè)直線斜率為
，直線
的斜率為
，則
等于
.
其中，正確命題的序號為_______.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
（a∈R且a≠0）.
（1）當(dāng)a
時，求曲線y＝f（x）在點（1，f（1））處的切線方程；
（2）討論函數(shù)f（x）的單調(diào)性與單調(diào)區(qū)間；
（3）若y＝f（x）有兩個極值點x1，x2，證明：f（x1）+f（x2）＜9﹣lna.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
