
【題目】為響應黨中央“扶貧攻堅”的號召,某單位指導一貧困村通過種植紫甘薯來提高經濟收入.紫甘薯對環境溫度要求較高,根據以往的經驗,隨著溫度的升高,其死亡株數成增長的趨勢.下表給出了2017年種植的一批試驗紫甘薯在溫度升高時6組死亡的株數:

經計算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分別為試驗數據中的溫度和死亡株數,
分別為試驗數據中的溫度和死亡株數, ![]() .
.
(1)若用線性回歸模型,求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() (結果精確到
(結果精確到![]() );
);
(2)若用非線性回歸模型求得![]() 關于
關于![]() 的回歸方程為
的回歸方程為![]() ,且相關指數為
,且相關指數為![]() .
.
(i)試與(1)中的回歸模型相比,用![]() 說明哪種模型的擬合效果更好;
說明哪種模型的擬合效果更好;
(ii)用擬合效果好的模型預測溫度為![]() 時該批紫甘薯死亡株數(結果取整數).
時該批紫甘薯死亡株數(結果取整數).
附:對于一組數據![]() ,
, ![]() ,……,
,……, ![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: 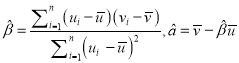 ;相關指數為:
;相關指數為: 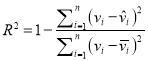 .
.
【答案】(Ⅰ) ![]() ;(Ⅱ)詳見解析.
;(Ⅱ)詳見解析.
【解析】試題分析:(1)利用回歸方程的公式,求得線性回歸方程為: ![]() =6.6x139.4;(2)(i)
=6.6x139.4;(2)(i)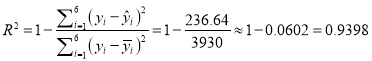 ,因為0.9398<0.9522,所以回歸方程
,因為0.9398<0.9522,所以回歸方程![]() 比線性回歸方程
比線性回歸方程![]() =6.6x138.6擬合效果更好;(ii)當溫度
=6.6x138.6擬合效果更好;(ii)當溫度![]() 時,
時, ![]() ,即當溫度為35C時該批紫甘薯死亡株數為190.
,即當溫度為35C時該批紫甘薯死亡株數為190.
試題解析:
(Ⅰ)由題意得, 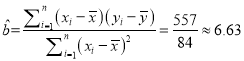
∴![]() 336.6326=139.4,
336.6326=139.4,
∴![]() 關于
關于![]() 的線性回歸方程為:
的線性回歸方程為: ![]() =6.6x139.4.
=6.6x139.4.
(注:若用![]() 計算出
計算出![]() ,則酌情扣1分)
,則酌情扣1分)
(Ⅱ) (i)線性回歸方程![]() =6.6x138.6對應的相關系數為:
=6.6x138.6對應的相關系數為:
 ,
,
因為0.9398<0.9522,
所以回歸方程![]() 比線性回歸方程
比線性回歸方程![]() =6.6x138.6擬合效果更好.
=6.6x138.6擬合效果更好.
(ii)由(i)知,當溫度![]() 時,
時,
![]() ,
,
即當溫度為35C時該批紫甘薯死亡株數為190.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】新型冠狀病毒肺炎![]() 疫情發生以來,在世界各地逐漸蔓延.在全國人民的共同努力和各級部門的嚴格管控下,我國的疫情已經得到了很好的控制.然而,小王同學發現,每個國家在疫情發生的初期,由于認識不足和措施不到位,感染人數都會出現快速的增長.下表是小王同學記錄的某國連續8天每日新型冠狀病毒感染確診的累計人數.
疫情發生以來,在世界各地逐漸蔓延.在全國人民的共同努力和各級部門的嚴格管控下,我國的疫情已經得到了很好的控制.然而,小王同學發現,每個國家在疫情發生的初期,由于認識不足和措施不到位,感染人數都會出現快速的增長.下表是小王同學記錄的某國連續8天每日新型冠狀病毒感染確診的累計人數.
日期代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累計確診人數 | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
為了分析該國累計感染人數的變化趨勢,小王同學分別用兩種模型:①![]() ,②
,②![]() 對變量
對變量![]() 和
和![]() 的關系進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差
的關系進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差![]() ):經過計算得
):經過計算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
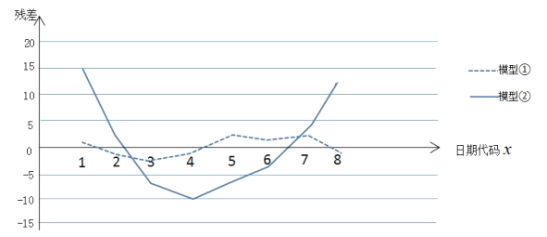
(1)根據殘差圖,比較模型①,②的擬合效果,應該選擇哪個模型?并簡要說明理由;
(2)根據(1)問選定的模型求出相應的回歸方程(系數均保留一位小數);
(3)由于時差,該國截止第9天新型冠狀病毒感染確診的累計人數尚未公布.小王同學認為,如果防疫形勢沒有得到明顯改善,在數據公布之前可以根據他在(2)問求出的回歸方程來對感染人數作出預測,那么估計該地區第9天新型冠狀病毒感染確診的累計人數是多少.
附:回歸直線的斜率和截距的最小二乘估計公式分別為: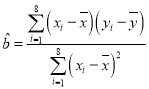 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了節能減排,發展低碳經濟,我國政府從2001年起就通過相關扶植政策推動新能源汽車產業發展.下面的圖表反映了該產業發展的相關信息:
中國新能源汽車產銷情況一覽表 | ||||
新能源汽車產量 | 新能源汽車銷量 | |||
產量(萬輛) | 比上年同期增長( | 銷量(萬輛) | 比上年同期增長( | |
2018年3月 | 6.8 | 105 | 6.8 | 117.4 |
4月 | 8.1 | 117.7 | 8.2 | 138.4 |
5月 | 9.6 | 85.6 | 10.2 | 125.6 |
6月 | 8.6 | 31.7 | 8.4 | 42.9 |
7月 | 9 | 53.6 | 8.4 | 47.7 |
8月 | 9.9 | 39 | 10.1 | 49.5 |
9月 | 12.7 | 64.4 | 12.1 | 54.8 |
10月 | 14.6 | 58.1 | 13.8 | 51 |
11月 | 17.3 | 36.9 | 16.9 | 37.6 |
1-12月 | 127 | 59.9 | 125.6 | 61.7 |
2019年1月 | 9.1 | 113 | 9.6 | 138 |
2月 | 5.9 | 50.9 | 5.3 | 53.6 |
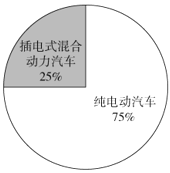
2019年2月份新能源汽車銷量結構圖
根據上述圖表信息,下列結論錯誤的是( )
A.2018年4月份我國新能源汽車的銷量高于產量
B.2017年3月份我國新能源汽車的產量不超過3.4萬輛
C.2019年2月份我國插電式混合動力汽車的銷量低于1萬輛
D.2017年我國新能源汽車總銷量超過70萬輛
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知
中,已知![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,且橢圓經過點
的左、右焦點,且橢圓經過點![]() 和點
和點![]() ,其中
,其中![]() 為橢圓的離心率.
為橢圓的離心率.

(1)求橢圓的方程;
(2)過點![]() 的直線
的直線![]() 橢圓于另一點
橢圓于另一點![]() ,點
,點![]() 在直線
在直線![]() 上,且
上,且![]() .若
.若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
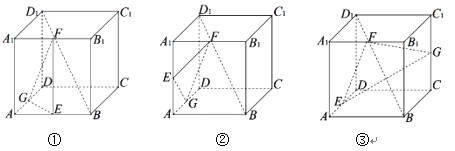
【題目】如圖,在下列三個正方體![]() 中,
中,![]() 均為所在棱的中點,過
均為所在棱的中點,過![]() 作正方體的截面.在各正方體中,直線
作正方體的截面.在各正方體中,直線![]() 與平面
與平面![]() 的位置關系描述正確的是
的位置關系描述正確的是
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面是正方形,每條側棱的長都是底面邊長的
的底面是正方形,每條側棱的長都是底面邊長的![]() 倍,
倍,![]() 為側棱
為側棱![]() 上的點.
上的點.
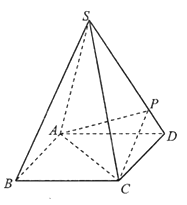
(1)求證:![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)在(2)的條件下,側棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() .若存在,求
.若存在,求![]() 的值;若不存在,試說明理由.
的值;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}滿足a3=2,前3項和為S3=![]() .
.
(1)求{an}的通項公式;
(2)設等比數列{bn}滿足b1=a1,b4=a15,求{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD的底面ABCD是矩形,PA⊥平面ABCD, PA=AD=2,E,F分別為PA,AB的中點,且DF⊥CE.
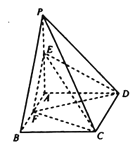
(1)求AB的長;
(2)求直線CF與平面DEF所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com