
【題目】新型冠狀病毒肺炎![]() 疫情發生以來,在世界各地逐漸蔓延.在全國人民的共同努力和各級部門的嚴格管控下,我國的疫情已經得到了很好的控制.然而,小王同學發現,每個國家在疫情發生的初期,由于認識不足和措施不到位,感染人數都會出現快速的增長.下表是小王同學記錄的某國連續8天每日新型冠狀病毒感染確診的累計人數.
疫情發生以來,在世界各地逐漸蔓延.在全國人民的共同努力和各級部門的嚴格管控下,我國的疫情已經得到了很好的控制.然而,小王同學發現,每個國家在疫情發生的初期,由于認識不足和措施不到位,感染人數都會出現快速的增長.下表是小王同學記錄的某國連續8天每日新型冠狀病毒感染確診的累計人數.
日期代碼 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累計確診人數 | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
為了分析該國累計感染人數的變化趨勢,小王同學分別用兩種模型:①![]() ,②
,②![]() 對變量
對變量![]() 和
和![]() 的關系進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差
的關系進行擬合,得到相應的回歸方程并進行殘差分析,殘差圖如下(注:殘差![]() ):經過計算得
):經過計算得![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
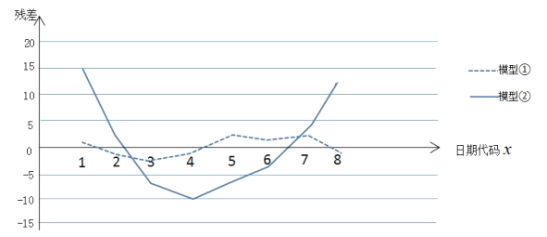
(1)根據殘差圖,比較模型①,②的擬合效果,應該選擇哪個模型?并簡要說明理由;
(2)根據(1)問選定的模型求出相應的回歸方程(系數均保留一位小數);
(3)由于時差,該國截止第9天新型冠狀病毒感染確診的累計人數尚未公布.小王同學認為,如果防疫形勢沒有得到明顯改善,在數據公布之前可以根據他在(2)問求出的回歸方程來對感染人數作出預測,那么估計該地區第9天新型冠狀病毒感染確診的累計人數是多少.
附:回歸直線的斜率和截距的最小二乘估計公式分別為: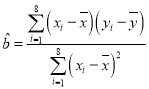 ,
,![]() .
.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知點
中,已知點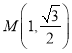 ,
,![]() 的參數方程為
的參數方程為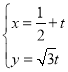 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某餐廳通過查閱了最近5次食品交易會參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下統計表:
(袋),得到如下統計表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會人數 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根據所給5組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)已知購買原材料的費用![]() (元)與數量
(元)與數量![]() (袋)的關系為
(袋)的關系為![]() ,
,
投入使用的每袋原材料相應的銷售收入為700元,多余的原材料只能無償返還,據悉本次交易大會大約有15萬人參加,根據(1)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費用).
原材料費用).
參考公式:  ,
, ![]() .
.
參考數據: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校為增加應屆畢業生就業機會,每年根據應屆畢業生的綜合素質和學業成績對學生進行綜合評估,已知某年度參與評估的畢業生共有2000名.其評估成績![]() 近似的服從正態分布
近似的服從正態分布![]() .現隨機抽取了100名畢業生的評估成績作為樣本,并把樣本數據進行了分組,繪制了如下頻率分布直方圖:
.現隨機抽取了100名畢業生的評估成績作為樣本,并把樣本數據進行了分組,繪制了如下頻率分布直方圖:
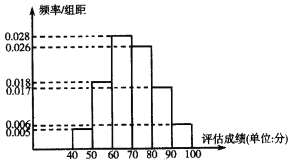
(1)求樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)若學校規定評估成績超過82.7分的畢業生可參加![]() 三家公司的面試.
三家公司的面試.
用樣本平均數![]() 作為的估計值
作為的估計值![]() ,用樣本標準差
,用樣本標準差![]() 作為
作為![]() 的估計值
的估計值![]() .請利用估計值判斷這2000名畢業生中,能夠參加三家公司面試的人數;
.請利用估計值判斷這2000名畢業生中,能夠參加三家公司面試的人數;
附:![]() 若隨機變量
若隨機變量![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前有聲書正受著越來越多人的喜愛.某有聲書公司為了解用戶使用情況,隨機選取了![]() 名用戶,統計出年齡分布和用戶付費金額(金額為整數)情況如下圖.
名用戶,統計出年齡分布和用戶付費金額(金額為整數)情況如下圖.
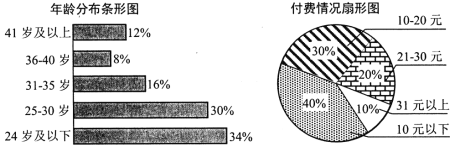
有聲書公司將付費高于![]() 元的用戶定義為“愛付費用戶”,將年齡在
元的用戶定義為“愛付費用戶”,將年齡在![]() 歲及以下的用戶定義為“年輕用戶”.已知抽取的樣本中有
歲及以下的用戶定義為“年輕用戶”.已知抽取的樣本中有![]() 的“年輕用戶”是“愛付費用戶”.
的“年輕用戶”是“愛付費用戶”.
(1)完成下面的![]() 列聯表,并據此資料,能否有
列聯表,并據此資料,能否有![]() 的把握認為用戶“愛付費”與其為“年輕用戶”有關?
的把握認為用戶“愛付費”與其為“年輕用戶”有關?
愛付費用戶 | 不愛付費用戶 | 合計 | |
年輕用戶 | |||
非年輕用戶 | |||
合計 |
(2)若公司采用分層抽樣方法從“愛付費用戶”中隨機選取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行訪談,求抽取的
人進行訪談,求抽取的![]() 人恰好都是“年輕用戶”的概率.
人恰好都是“年輕用戶”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
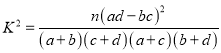 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生身高情況,某校以10%的比例對全校700名學生按性別進行分層抽樣檢查,測得身高情況的統計圖如下:
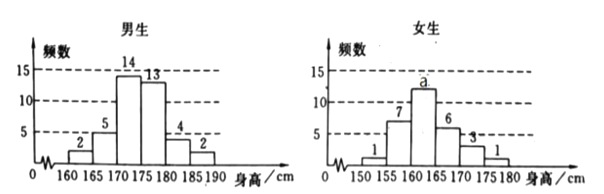
(1)估計該校男生的人數;并求出![]() 值
值
(2)估計該校學生身高在![]() 之間的概率;
之間的概率;
(3)從樣本中身高在![]() 之間的女生中任選2人,求至少有1人身高在
之間的女生中任選2人,求至少有1人身高在![]() 之間的概率。
之間的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應黨中央“扶貧攻堅”的號召,某單位指導一貧困村通過種植紫甘薯來提高經濟收入.紫甘薯對環境溫度要求較高,根據以往的經驗,隨著溫度的升高,其死亡株數成增長的趨勢.下表給出了2017年種植的一批試驗紫甘薯在溫度升高時6組死亡的株數:

經計算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分別為試驗數據中的溫度和死亡株數,
分別為試驗數據中的溫度和死亡株數, ![]() .
.
(1)若用線性回歸模型,求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() (結果精確到
(結果精確到![]() );
);
(2)若用非線性回歸模型求得![]() 關于
關于![]() 的回歸方程為
的回歸方程為![]() ,且相關指數為
,且相關指數為![]() .
.
(i)試與(1)中的回歸模型相比,用![]() 說明哪種模型的擬合效果更好;
說明哪種模型的擬合效果更好;
(ii)用擬合效果好的模型預測溫度為![]() 時該批紫甘薯死亡株數(結果取整數).
時該批紫甘薯死亡株數(結果取整數).
附:對于一組數據![]() ,
, ![]() ,……,
,……, ![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: 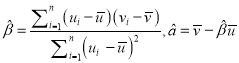 ;相關指數為:
;相關指數為: 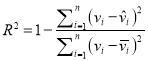 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com