
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為: (
(![]() 為參數),在以
為參數),在以![]() 為極點,
為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 的坐標為
的坐標為![]() ,求
,求![]() .
.
 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源: 題型:
【題目】若實數![]() 滿足
滿足![]() ,則稱
,則稱![]() 比
比![]() 接近
接近![]()
(1)若4比![]() 接近0,求
接近0,求![]() 的取值范圍;
的取值范圍;
(2)對于任意的兩個不等正數![]() ,求證:
,求證:![]() 比
比![]() 接近
接近![]() ;
;
(3)若對于任意的非零實數![]() ,實數
,實數![]() 比
比![]() 接近
接近![]() ,求
,求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據下列條件,求圓的標準方程:
(1)已知點A(1,1),B(﹣1,3),且AB是圓的直徑,求圓的標準方程;
(2)圓與y軸交于A(0,﹣4),B(0,﹣2),圓心在直線2x﹣y﹣7=0上,求圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四位同學一起去向老師詢問成語競賽的成績,老師說:“你們四人中有![]() 位優秀,
位優秀,![]() 位良好,我現在給甲看乙、丙的成績,給乙看丙的成績,給丁看甲的成績.”看后甲對大家說:“我還是不知道我的成績.”根據以上信息,則( )
位良好,我現在給甲看乙、丙的成績,給乙看丙的成績,給丁看甲的成績.”看后甲對大家說:“我還是不知道我的成績.”根據以上信息,則( )
A.乙可以知道兩人的成績B.丁可能知道兩人的成績
C.乙、丁可以知道自己的成績D.乙、丁可以知道對方的成績
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《福建省高考改革試點方案》規定:從2018年秋季高中入學的新生開始,不分文理科;2021年開始,高考總成績由語數外3門統考科目和物理、化學等六門選考科目構成,將每門選考科目的考生原始成績從高到低劃分為A、B+、B、C+、C、D+、D、E共8個等級,參照正態分布原則,確定各等級人數所占比例分別為3%、7%、18%、22%、22%、18%、7%、3%,選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到[91,100]、[81,90]、[71.80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八個分數區間,得到考生的等級成績,某校高一年級共2000人,為給高一學生合理選科提供依據,對六門選考科目進行測試,其中化學考試原始成績![]() 基本服從正態分布
基本服從正態分布![]() .
.
(1)求化學原始成績在區間(57,96)的人數;
(2)以各等級人數所占比例作為各分數區間發生的概率,按高考改革方案,若從全省考生中隨機抽取3人,記![]() 表示這3人中等級成績在區間[71,90]的人數,求事件
表示這3人中等級成績在區間[71,90]的人數,求事件![]() 的概率
的概率
(附:若隨機變量![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是圓的直徑,PA垂直圓所在的平面,C是圓上的點.

(1)求證:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 如圖,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的中點,沿
的中點,沿![]() 將
將![]() 折起,得到如圖所示的四棱錐
折起,得到如圖所示的四棱錐![]()

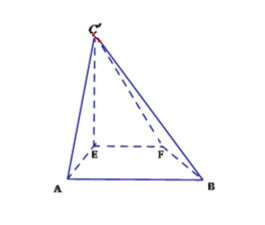
(1)求證:![]() 平面
平面![]() ;
;
(2)當四棱錐![]() 體積取最大值時,
體積取最大值時,
(i) 寫出最大體積;
(ii) 求![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點為極點,![]() 軸的正半軸為極軸建立極坐標系,兩種坐標系取相同的單位長度.已知曲線
軸的正半軸為極軸建立極坐標系,兩種坐標系取相同的單位長度.已知曲線![]() ,過點
,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為 .直線
.直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 、
、![]() .
.
(1)求![]() 的取值范圍;
的取值范圍;
(2)若![]() 、
、![]() 、
、![]() 成等比數列,求實數
成等比數列,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某機械廠欲從![]() 米,
米,![]() 米的矩形鐵皮中裁剪出一個四邊形
米的矩形鐵皮中裁剪出一個四邊形![]() 加工成某儀器的零件,裁剪要求如下:點
加工成某儀器的零件,裁剪要求如下:點![]() 分別在邊
分別在邊![]() 上,且
上,且![]() ,
,![]() .設
.設![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() (單位:平方米).
(單位:平方米).

(1)求![]() 關于
關于![]() 的函數關系式,求出定義域;
的函數關系式,求出定義域;
(2)當![]() 的長為何值時,裁剪出的四邊形
的長為何值時,裁剪出的四邊形![]() 的面積最小,并求出最小值.
的面積最小,并求出最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com