
分析 (1)利用等差數列與等比數列的通項公式即可得出.
(2)利用“裂項求和”方法、數列的單調性即可證明.
解答 (1)解:∵a1=1,an+1=an+c(c為常數,n∈N+,
∴a2=1+c,a5=1+4c.
∵a1,a2,a5成公比q≠1的等比數列,∴${a}_{2}^{2}$=a1a5.
∴(1+c)2=1×(1+4c),解得c=0,或2.
c=0時,q=1,舍去.
∴c=2.
(2)證明:∵an+1=an+2,可得:an+1-an=2.
∴an=1+2(n-1)=2n-1.
∵an•an+1•bn=1,∴bn=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$$(\frac{1}{2n-1}-\frac{1}{2n+1})$.
∴數列{bn}的前n項和為Sn=$\frac{1}{2}$$[(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}$$(1-\frac{1}{2n+1})$<$\frac{1}{2}$.
又數列$\{-\frac{1}{2n+1}\}$單調遞增,∴Sn≥S1=$\frac{1}{2}×(1-\frac{1}{3})$=$\frac{1}{3}$.
∴$\frac{1}{3}$≤Sn<$\frac{1}{2}$.
點評 本題考查了等差數列與等比數列的通項公式、“裂項求和”方法、數列的單調性,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | (1.4,2) | B. | (1,1.4) | C. | (1,1.5) | D. | (1.5,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
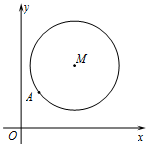 如圖,在平面直角坐標系xOy中,已知以M為圓心的圓M:x2+y2-12x-14y+60=0及其上一點A(2,4).
如圖,在平面直角坐標系xOy中,已知以M為圓心的圓M:x2+y2-12x-14y+60=0及其上一點A(2,4).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x0∈N | B. | x0∉N | C. | x0∈N或x0∉N | D. | 不能確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
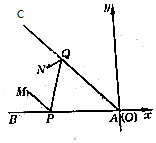 如圖,∠BAC為伸入江中的半島,AB和AC為兩江岸,M處為水文站,N處為電訊局,現欲在兩江岸AB和AC上各建一個水文觀測點P、Q,現測得∠BAC=45°,當直角坐標系以點A為坐標原點且以直線BA為x軸時,測得M(-4,1)、N(-3,2).P、Q兩點應建在何處才能使路程MPQN最短?
如圖,∠BAC為伸入江中的半島,AB和AC為兩江岸,M處為水文站,N處為電訊局,現欲在兩江岸AB和AC上各建一個水文觀測點P、Q,現測得∠BAC=45°,當直角坐標系以點A為坐標原點且以直線BA為x軸時,測得M(-4,1)、N(-3,2).P、Q兩點應建在何處才能使路程MPQN最短?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com