
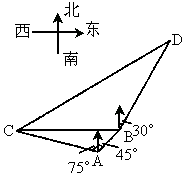
如圖,在海岸A處,發現北偏東45°方向,距A為(3-1)海里的B處有一走私船,在A處北偏西75°方向,距A為2海里的C處的緝私船奉命以103海里/時的速度追截走私船,此時走私船正以10海里/時的速度從B處向北偏東30°方向逃竄,問緝私船沿什么方向能最快追上走私船,并求出所需要的時間.

|
解:設緝私船追上走私船所需的時間為t小時,則CD=10 在△ABC中,∵AB= 由余弦定理,得BC= 由正弦定理,得sin∠ABC= ∴∠ABC=45°,易知CB方向與正北方向垂直,則∠CBD=90°+30°=120°. 在△BCD中,由正弦定理,得sin∠BCD= ∴∠BCD=30°,∠BDC=30°. ∴BD=BC= ∴10t=6,即t= ∴緝私船沿北偏東60°方向能最快追上走私船,需要 思路分析:設經過t小時后,緝私船能最快追上走私船,即在圖中的D處恰好兩船相遇,CD方向即是緝私船的追截方向,利用正、余弦定理根據條件解三角形. |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:數學教研室 題型:044
如下圖,在海岸A處,發現北偏東45°方向,距A為 的B處有一艘走私船,在A處北偏西75°方向,距A為2 n mile的C處的緝私船奉命以
的B處有一艘走私船,在A處北偏西75°方向,距A為2 n mile的C處的緝私船奉命以 的速度追截走私船,此時走私船正以10 n mile/h的速度從B處向北偏東30°方向逃竄,問緝私船沿什么方向能最快追上走私船,并求出所需要的時間?
的速度追截走私船,此時走私船正以10 n mile/h的速度從B處向北偏東30°方向逃竄,問緝私船沿什么方向能最快追上走私船,并求出所需要的時間?

查看答案和解析>>
科目:高中數學 來源: 題型:044
如下圖,在海岸
A處,發現北偏東45°方向,距A為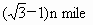 的B處有一艘走私船,在A處北偏西75°方向,距A為2 n mile的C處的緝私船奉命以
的B處有一艘走私船,在A處北偏西75°方向,距A為2 n mile的C處的緝私船奉命以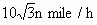 的速度追截走私船,此時走私船正以10 n mile/h的速度從B處向北偏東30°方向逃竄,問緝私船沿什么方向能最快追上走私船,并求出所需要的時間?
的速度追截走私船,此時走私船正以10 n mile/h的速度從B處向北偏東30°方向逃竄,問緝私船沿什么方向能最快追上走私船,并求出所需要的時間?
查看答案和解析>>
科目:高中數學 來源:設計必修五數學北師版 北師版 題型:044
如圖,在海岸A處,發現北偏東45°方向,距A為(3-1)海里的B處有一走私船,在A處北偏西75°方向,距A為2海里的C處的緝私船奉命以103海里/時的速度追截走私船,此時走私船正以10海里/時的速度從B處向北偏東30°方向逃竄,問緝私船沿什么方向能最快追上走私船?并求出所需要的時間.

查看答案和解析>>
科目:高中數學 來源:同步題 題型:解答題
 -1)km的B處有一艘走私船,在A處北偏西75°方向且距A為2km的C處的緝私船奉命以10
-1)km的B處有一艘走私船,在A處北偏西75°方向且距A為2km的C處的緝私船奉命以10 km/h的速度追緝走私船。此時走私船正以10km/h的速度從B處向北偏東30°方向逃竄,則緝私船沿什么方向能最快追上走私船?并求出所需要的時間。
km/h的速度追緝走私船。此時走私船正以10km/h的速度從B處向北偏東30°方向逃竄,則緝私船沿什么方向能最快追上走私船?并求出所需要的時間。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com