
【題目】在平面直角坐標系xOy中,已知曲線C1:![]() (t為參數),C2:
(t為參數),C2: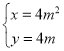 (m為參數).
(m為參數).
(1)將C1,C2的方程化為普通方程,并說明它們分別表示什么曲線;
(2)設曲線C1與C2的交點分別為A,B,O為坐標原點,求△OAB的面積的最小值.
【答案】(1)![]() sinθx-cosθy﹣2sin θ=0,
sinθx-cosθy﹣2sin θ=0,![]() y2=4x,(2)4
y2=4x,(2)4![]() .
.
【解析】
(1)C1:將![]() 兩邊同時乘以
兩邊同時乘以![]() 將
將![]() 兩邊同時乘以
兩邊同時乘以![]() ,消去參數t即可,C2消去m即可;
,消去參數t即可,C2消去m即可;
(2)聯立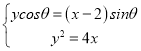 得y2sinθ﹣4ycosθ﹣8sinθ=0,設A(x1,y1),B(x2,y2),則y1+y2
得y2sinθ﹣4ycosθ﹣8sinθ=0,設A(x1,y1),B(x2,y2),則y1+y2![]() ,y1y2=﹣8,代入S△OAB=
,y1y2=﹣8,代入S△OAB=![]() |y1﹣y2|計算即可.
|y1﹣y2|計算即可.
(1)由C1:![]() (t為參數)消去t得C1:cosθy=sinθ(x﹣2),得sinθx-cosθy-2sinθ=0,
(t為參數)消去t得C1:cosθy=sinθ(x﹣2),得sinθx-cosθy-2sinθ=0,
由C2: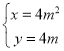 (m為參數)消去m得C2:y2=4x,
(m為參數)消去m得C2:y2=4x,
(2)聯立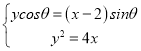 消去x得y2sinθ﹣4ycosθ﹣8sinθ=0,
消去x得y2sinθ﹣4ycosθ﹣8sinθ=0,
設A(x1,y1),B(x2,y2),則y1+y2![]() ,y1y2=﹣8,又C1與x軸的交點(2,0)
,y1y2=﹣8,又C1與x軸的交點(2,0)
∴S△OAB=![]() |y1﹣y2|
|y1﹣y2|![]()
![]()
=![]() ,
,
所以 sinθ=1時,SOAB取得最小值4![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某企業擬生產一種如圖所示的圓柱形易拉罐(上下底面及側面的厚度不計),易拉罐的體積為![]() ,設圓柱的高度為
,設圓柱的高度為![]() ,底面半徑為
,底面半徑為![]() ,且
,且![]() ,假設該易拉罐的制造費用僅與其表面積有關.已知易拉罐側面制造費用為
,假設該易拉罐的制造費用僅與其表面積有關.已知易拉罐側面制造費用為![]() 元
元![]() ,易拉罐上下底面的制造費用均為
,易拉罐上下底面的制造費用均為![]() 元
元![]() 為常數).
為常數).
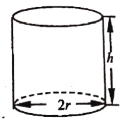
(1)寫出易拉罐的制造費用![]() (元)關于
(元)關于![]() 的函數表達式,并求其定義域;
的函數表達式,并求其定義域;
(2)求易拉罐制造費用最低時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 為左右焦點,
為左右焦點,![]() 為短軸端點,長軸長為4,焦距為
為短軸端點,長軸長為4,焦距為![]() ,且
,且![]() ,
,![]() 的面積為
的面積為![]() .
.
(Ⅰ)求橢圓![]() 的方程
的方程
(Ⅱ)設動直線![]() 橢圓
橢圓![]() 有且僅有一個公共點
有且僅有一個公共點![]() ,且與直線
,且與直線![]() 相交于點
相交于點![]() .試探究:在坐標平面內是否存在定點
.試探究:在坐標平面內是否存在定點![]() ,使得以
,使得以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在求出點
?若存在求出點![]() 的坐標,若不存在.請說明理由.
的坐標,若不存在.請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用0與1兩個數字隨機填入如圖所示的5個格子里,每個格子填一個數字,并且從左到右數,不管數到哪個格子,總是1的個數不少于0的個數,則這樣填法的概率為__________.
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 務極點,
務極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() ,
,![]()
(1)求曲線![]() ,
,![]() 的直角坐標方程;
的直角坐標方程;
(2)曲線![]() 和
和![]() 的交點為
的交點為![]() ,
,![]() ,求以
,求以![]() 為直徑的圓與
為直徑的圓與![]() 軸的交點坐標.
軸的交點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() .現沿對角線
.現沿對角線![]() 將
將![]() 折起,使點
折起,使點![]() 到達點
到達點![]() .點
.點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,且
上,且![]() 、
、![]() 、
、![]() 、
、![]() 四點共面.
四點共面.

(1)求證:![]() ;
;
(2)若平面![]() 平面
平面![]() ,平面
,平面![]() 與平面
與平面![]() 夾角為
夾角為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x-1,![]() (a∈R),若對任意x1∈[1,+∞),總存在x2∈R,使f(x1)=g(x2),則實數a的取值范圍是( )
(a∈R),若對任意x1∈[1,+∞),總存在x2∈R,使f(x1)=g(x2),則實數a的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com