Question

已知函數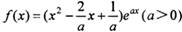

(1) 求曲線在點A（0，)處的切線方程；

(2) 討論函數的單調性；

(3) 是否存在實數，使當時恒成立？若存在，求出實數a;若不存在，請說明理由.

 

Answer 1

【答案】

（1）∵ a＞0，，

∴

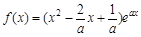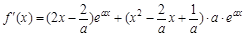
=，                …………… 2分

于是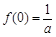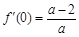，，所以曲線y = f（x）在點A（0，f（0））處的切線方程為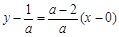，即（a－2）x－ay + 1 = 0．                    … 4分

（2）∵ a＞0，e^ax＞0，∴ 只需討論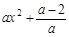的符號．            ………… 5分

ⅰ）當a＞2時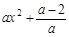，＞0，這時f ′（x）＞0，所以函數f（x）在（－∞，+∞）上為增函數．

ⅱ）當a = 2時，f ′（x）= 2x²e^2x≥0，函數f（x）在（－∞，+∞）上為增函數．

ⅲ）當0＜a＜2時，令f ′（x）= 0，解得，．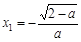

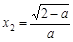當x變化時， f '（x）和f（x）的變化情況如下表：

x
f '（x）	+	0	－	0	+
f（x）	↗	極大值	↘	極小值	↗

∴ f（x）在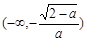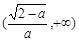，為增函數，

f（x）在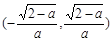為減函數．

（3）當a∈（1，2）時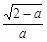，∈（0，1）．由（2）知f（x）在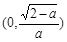上是減函數，在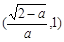上是增函數，故當x∈（0，1）時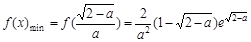，，所以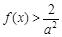當x∈（0，1）時恒成立，等價于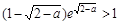恒成立．當a∈（1，2）時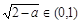，，設，則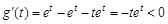，表明g(t) 在（0，1）上單調遞減，于是可得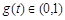，即a∈（1，2）時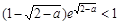恒成立，因此，符合條件的實數a不存在．

【解析】略