
【題目】在公差不為零的等差數(shù)列![]() 中,已知
中,已知![]() ,且
,且![]() 依次成等比數(shù)列.數(shù)列
依次成等比數(shù)列.數(shù)列![]() 滿足
滿足![]() ,且
,且![]() .
.
(1)求數(shù)列![]() ,
, ![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)求數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() .
.
【答案】(1)![]() ,
, ![]() ;
;
(2)![]()
【解析】試題分析:(1)由已知條件推導(dǎo)出![]() ,由此能求出數(shù)列
,由此能求出數(shù)列![]() 的通項(xiàng)公式,在數(shù)列
的通項(xiàng)公式,在數(shù)列![]() 中,由
中,由![]() ,得
,得![]() ,由此能求出數(shù)列的
,由此能求出數(shù)列的![]() 通項(xiàng)公式;(2)由(1)得
通項(xiàng)公式;(2)由(1)得![]() ,由此利用錯位相減法求出
,由此利用錯位相減法求出![]() .
.
試題解析:(1)因?yàn)?/span>![]() 依次成等比數(shù)列,所以可得
依次成等比數(shù)列,所以可得![]() ,
, ![]() ;
;
(2)![]() ,
, ![]()
![]() ,以上兩式相減,整理可得
,以上兩式相減,整理可得
![]()
【易錯點(diǎn)晴】本題主要考察等差數(shù)列的通項(xiàng)公式,等比數(shù)列的通項(xiàng)公式以及“錯位相減法”求數(shù)列的和,屬于難題. “錯位相減法”求數(shù)列的和是重點(diǎn)也是難點(diǎn),利用“錯位相減法”求數(shù)列的和應(yīng)注意以下幾點(diǎn):①掌握運(yùn)用“錯位相減法”求數(shù)列的和的條件(一個等差數(shù)列與一個等比數(shù)列的積);②相減時(shí)注意最后一項(xiàng) 的符號;③求和時(shí)注意項(xiàng)數(shù)別出錯;④最后結(jié)果一定不能忘記等式兩邊同時(shí)除以![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(Ⅱ)若![]() 對
對![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)求整數(shù)![]() 的值,使函數(shù)
的值,使函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有零點(diǎn).
上有零點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)當(dāng)![]() 時(shí),是否存在正實(shí)數(shù)
時(shí),是否存在正實(shí)數(shù)![]() ,當(dāng)
,當(dāng)![]() (
(![]() 是自然對數(shù)底數(shù))時(shí),函數(shù)
是自然對數(shù)底數(shù))時(shí),函數(shù)![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,公園有一塊邊長為![]() 的等邊
的等邊![]() 的邊角地,現(xiàn)修成草坪,圖中
的邊角地,現(xiàn)修成草坪,圖中![]() 把草坪分成面積相等的兩部分,
把草坪分成面積相等的兩部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.

(1)設(shè)![]() (
(![]() ),
),![]() ,求用
,求用![]() 表示
表示![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)如果![]() 是灌溉水管,為節(jié)約成本,希望它最短,
是灌溉水管,為節(jié)約成本,希望它最短,![]() 的位置應(yīng)在哪里?如果
的位置應(yīng)在哪里?如果![]() 是參觀線路,則希望它最長,
是參觀線路,則希望它最長,![]() 的位置又應(yīng)在哪里?請說明理由.
的位置又應(yīng)在哪里?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校隨機(jī)抽取部分新生調(diào)查其上學(xué)路上所需時(shí)間(單位:分鐘),并將所得數(shù)據(jù)繪制成頻率分布直方圖(如圖),其中,上學(xué)路上所需時(shí)間的范圍是![]() ,樣本數(shù)據(jù)分組為
,樣本數(shù)據(jù)分組為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方圖中![]() 的值;
的值;
(2)如果上學(xué)路上所需時(shí)間不少于60分鐘的學(xué)生可申請?jiān)趯W(xué)校住宿,請估計(jì)學(xué)校1000名新生中有多少名學(xué)生可以申請住宿;
(3)現(xiàn)有6名上學(xué)路上時(shí)間小于![]() 分鐘的新生,其中2人上學(xué)路上時(shí)間小于
分鐘的新生,其中2人上學(xué)路上時(shí)間小于![]() 分鐘. 從這6人中任選2人,設(shè)這2人中上學(xué)路上時(shí)間小于
分鐘. 從這6人中任選2人,設(shè)這2人中上學(xué)路上時(shí)間小于![]() 分鐘人數(shù)為
分鐘人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高二(1)班的一次數(shù)學(xué)測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如下,且將全班25人的成績記為![]() 由右邊的程序運(yùn)行后,輸出
由右邊的程序運(yùn)行后,輸出![]() .據(jù)此解答如下問題:
.據(jù)此解答如下問題:
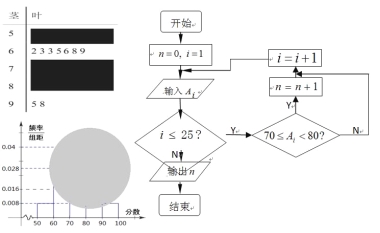
(Ⅰ)求莖葉圖中破損處分?jǐn)?shù)在[50,60),[70,80),[80,90)各區(qū)間段的頻數(shù);
(Ⅱ)利用頻率分布直方圖估計(jì)該班的數(shù)學(xué)測試成績的眾數(shù),中位數(shù)分別是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】通過研究學(xué)生的學(xué)習(xí)行為,心理學(xué)家發(fā)現(xiàn),學(xué)生接受能力依賴于老師引入概念和描述問題所用的時(shí)間,講座開始時(shí),學(xué)生的興趣激增,中間有一段不太長的時(shí)間,學(xué)生的興趣保持理想的狀態(tài),隨后學(xué)生的注意力開始分散,分析結(jié)果和實(shí)驗(yàn)表明,用![]() 表示學(xué)生掌握和接受概念的能力(
表示學(xué)生掌握和接受概念的能力(![]() 的值越大,表示接受能力越強(qiáng)),
的值越大,表示接受能力越強(qiáng)),![]() 表示提出和講授概念的時(shí)間(單位:分),可以有以下公式:
表示提出和講授概念的時(shí)間(單位:分),可以有以下公式: 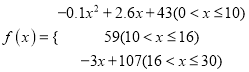 .
.
(1)開講多少分鐘后,學(xué)生的接受能力最強(qiáng)?能維持多少分鐘?
(2)開講5分鐘與開講20分鐘比較,學(xué)生的接受能力何時(shí)強(qiáng)一些?
(3)一個數(shù)學(xué)難題,需要55的接受能力以及13分鐘的時(shí)間,老師能否及時(shí)在學(xué)生一直達(dá)到所需接受能力的狀態(tài)下講授完這個難題?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 是公差為正數(shù)的等差數(shù)列,其前
是公差為正數(shù)的等差數(shù)列,其前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() ,
,![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)數(shù)列![]() 滿足
滿足![]() ,
,![]() .
.
①求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
②是否存在正整數(shù)![]() ,使得
,使得![]() 成等差數(shù)列?若存在,求出
成等差數(shù)列?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com