
【題目】已知函數![]() (
(![]() ).
).
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)當![]() 時,是否存在正實數
時,是否存在正實數![]() ,當
,當![]() (
(![]() 是自然對數底數)時,函數
是自然對數底數)時,函數![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點為
的兩個焦點為![]() ,
,![]() ,離心率為
,離心率為![]() ,點
,點![]() ,
,![]() 在橢圓上,
在橢圓上,![]() 在線段
在線段![]() 上,且
上,且![]() 的周長等于
的周長等于![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過圓![]() 上任意一點
上任意一點![]() 作橢圓
作橢圓![]() 的兩條切線
的兩條切線![]() 和
和![]() 與圓
與圓![]() 交于點
交于點![]() ,
,![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校一個生物興趣小組對學校的人工湖中養殖的某種魚類進行觀測研究,在飼料充足的前提下,興趣小組對飼養時間x(單位:月)與這種魚類的平均體重y(單位:千克)得到一組觀測值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在給出的坐標系中,畫出關于x、y兩個相關變量的散點圖.
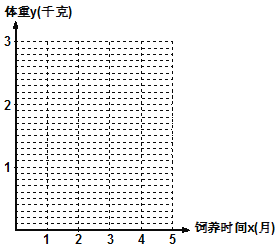
(2)請根據上表提供的數據,用最小二乘法求出變量![]() 關于變量
關于變量![]() 的線性回歸直線方程
的線性回歸直線方程![]() .
.
(3)預測飼養滿12個月時,這種魚的平均體重(單位:千克).
(參考公式: 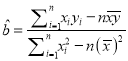 ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果y=f(x)的定義域為R,對于定義域內的任意x,存在實數a使得f(x+a)=f(﹣x)成立,則稱此函數具有“P(a)性質”.給出下列命題:
①函數y=sinx具有“P(a)性質”;
②若奇函數y=f(x)具有“P(2)性質”,且f(1)=1,則f(2015)=1;
③若函數y=f(x)具有“P(4)性質”,圖象關于點(1,0)成中心對稱,且在(﹣1,0)上單調遞減,則y=f(x)在(﹣2,﹣1)上單調遞減,在(1,2)上單調遞增;
④若不恒為零的函數y=f(x)同時具有“P(0)性質”和“P(3)性質”,函數y=f(x)是周期函數.
其中正確的是 (寫出所有正確命題的編號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】英州市育才中學對全體教師在教學中是否經常使用信息技術實施教學的情況進行了調查得到統計數據如下(表)
教師教齡 |
|
|
|
|
教師人數 |
|
|
|
|
經常使用信息技術實施教學的人數 |
|
|
|
|
(1)求該校教師在教學中不經常使用信息技術實施教學的概率;
(2)在教齡![]() 年以下,且經常使用信息技術教學的教師中任選
年以下,且經常使用信息技術教學的教師中任選![]() 人,其中恰有一人教齡在
人,其中恰有一人教齡在![]() 年以下的概率是多少?
年以下的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,橢圓
,橢圓![]() 過點
過點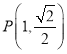 ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,且
,且![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是橢圓
是橢圓![]() 的上頂點,過點
的上頂點,過點![]() 分別作直線
分別作直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,設這兩條直線的斜率分別為
兩點,設這兩條直線的斜率分別為![]() ,且
,且![]() ,證明:直線
,證明:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數,(1)求
為奇函數,(1)求![]() 的值;(2)判斷并證明函數
的值;(2)判斷并證明函數![]() 的單調性;(3)是否存在這樣的實數
的單調性;(3)是否存在這樣的實數![]() ,使
,使![]() 對一切
對一切![]() 恒成立,若存在,試求出
恒成立,若存在,試求出![]() 取值的集合;若不存在,說明理由.
取值的集合;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com