
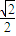 x,作DG⊥BB1,HG⊥CC1,EI⊥CC1,從而用x表示出EG,FI,,FH,從而將問題轉化到Rt△DHF中,有DF2=DH2+FH2求解.
x,作DG⊥BB1,HG⊥CC1,EI⊥CC1,從而用x表示出EG,FI,,FH,從而將問題轉化到Rt△DHF中,有DF2=DH2+FH2求解.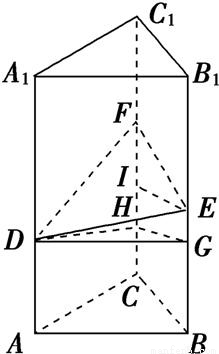 解:如圖,正三棱柱ABC-A1B1C1中,△ABC為正三角形,邊長為2,△DEF為等腰直角三角形,DF為斜邊,設DF長為x,則DE=EF=
解:如圖,正三棱柱ABC-A1B1C1中,△ABC為正三角形,邊長為2,△DEF為等腰直角三角形,DF為斜邊,設DF長為x,則DE=EF=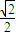 x,作DG⊥BB1,HG⊥CC1,EI⊥CC1,
x,作DG⊥BB1,HG⊥CC1,EI⊥CC1,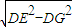 =
=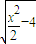 ,FI=
,FI=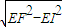 =
=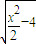 ,FH=FI+HI=FI+EG=2
,FH=FI+HI=FI+EG=2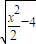 ,在Rt△DHF中,DF2=DH2+FH2,即x2=4+(2
,在Rt△DHF中,DF2=DH2+FH2,即x2=4+(2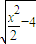 )2,解得x=2
)2,解得x=2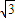 .
.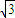 .
.

 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:
 如圖,一個等腰直角三角形的硬紙片△ABC中,∠ACB=90°,AC=4cm,CD是斜邊上的高,沿CD把△ABC折成直二面角.
如圖,一個等腰直角三角形的硬紙片△ABC中,∠ACB=90°,AC=4cm,CD是斜邊上的高,沿CD把△ABC折成直二面角.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•廣州二模)如圖,一個等腰直角三角形的直角邊長為2,分別以三個頂點為 圓心,l為半徑在三角形內作圓弧,三段圓弧與斜邊圍成區域M (圖中白色部分).若在此三角形內隨機取一點P,則點P落在區 域M內的概率為
(2013•廣州二模)如圖,一個等腰直角三角形的直角邊長為2,分別以三個頂點為 圓心,l為半徑在三角形內作圓弧,三段圓弧與斜邊圍成區域M (圖中白色部分).若在此三角形內隨機取一點P,則點P落在區 域M內的概率為| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com