
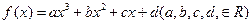 的圖像關于原點對稱,且x=1
的圖像關于原點對稱,且x=1 時,f(x)取極小值
時,f(x)取極小值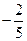 .
. 論.
論.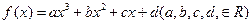 的圖像關于原點對稱,
的圖像關于原點對稱,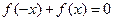 對任意
對任意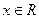 恒成立,
恒成立,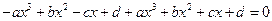 對任意
對任意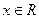 恒成立,
恒成立,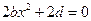 恒成立,故
恒成立,故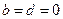 ,…………………3分
,…………………3分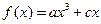 ,
,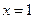 時,
時,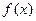 取極小值
取極小值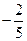 ,所以
,所以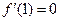 ,且
,且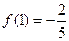 ,
,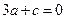 ………………①
………………①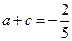 ……………………②
……………………②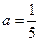 ,
,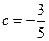 ;
;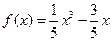 ,(
,(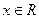 )…………………………………………………6分
)…………………………………………………6分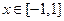 時,圖像上不存在兩點使得過此兩點處的切線互相垂直.
時,圖像上不存在兩點使得過此兩點處的切線互相垂直.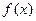 的圖像上存在兩點
的圖像上存在兩點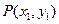 ,
,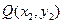 ,使得在此兩點處的切線互相垂直,由(Ⅰ) 可知
,使得在此兩點處的切線互相垂直,由(Ⅰ) 可知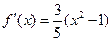 ,且在
,且在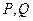 兩點處的切線斜率均存在.
兩點處的切線斜率均存在. 則有
則有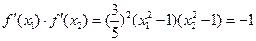 ,…………………………8分
,…………………………8分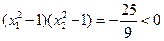 ,
,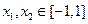 ,所以
,所以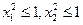 ,所以
,所以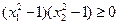 ,
,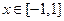 時,圖像上不存在兩點使得在此兩點處的切線互相垂直.………………12分
時,圖像上不存在兩點使得在此兩點處的切線互相垂直.………………12分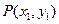 ,
,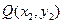 為
為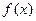 的圖像上兩點,由(Ⅰ) 可知
的圖像上兩點,由(Ⅰ) 可知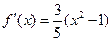 ,
,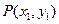 和點
和點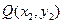 處的兩條切線的斜率均存在.
處的兩條切線的斜率均存在. 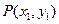 處的切線斜率為
處的切線斜率為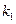 ,在點
,在點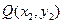 處的切線斜率為
處的切線斜率為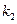 ,
,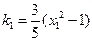 ,
,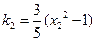 ;………………8分
;………………8分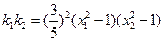 ,
,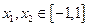 ,
,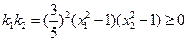 ,即
,即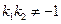
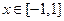 時,圖像上不存在兩點使得在此兩點處的切線互相垂直.……12分
時,圖像上不存在兩點使得在此兩點處的切線互相垂直.……12分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com